1. 如图,按照上北下南,左西右东的规定画出方向十字线,∠AOE = $m^{\circ}$,∠EOF = $90^{\circ}$,OM,ON 分别平分∠AOE 和∠BOF,有下列说法:①点 E 位于点 O 的北偏西 $m^{\circ}$;②图中互余的角有 4 对;③若∠BOF = 4∠AOE,则∠DON = $54^{\circ}$;④若 $\frac{∠MON}{∠AOE + ∠BOF} = n$,则 n 的倒数是 $\frac{2}{3}$。其中正确的有(
A.3 个
B.2 个
C.1 个
D.0 个
B
)A.3 个
B.2 个
C.1 个
D.0 个
答案:1. B 点拨:因为$∠AOE=m^{\circ }$,所以$∠EOD=90^{\circ }-m^{\circ }$,所以点 E 位于点 O 的北偏西$90^{\circ }-m^{\circ }$,故①错误;因为$∠EOF=90^{\circ }$,所以$∠EOD+∠DOF=90^{\circ }$,$∠AOE+∠BOF=90^{\circ }$。因为$∠AOD=∠BOD=90^{\circ }$,所以$∠AOE+∠EOD=90^{\circ }$,$∠DOF+∠FOB=90^{\circ }$,$∠AOM+∠MOD=90^{\circ }$,$∠BON+∠DON=90^{\circ }$。因为 OM,ON 分别平分$∠AOE$和$∠BOF$,所以$∠AOM=∠EOM$,$∠BON=∠FON$,所以$∠EOM+∠MOD=90^{\circ }$,$∠FON+∠DON=90^{\circ }$,所以题图中互余的角共有 8 对,故②错误;因为$∠BOF=4∠AOE$,$∠AOE+∠BOF=90^{\circ }$,所以$∠BOF=72^{\circ }$,所以$∠BON=36^{\circ }$,所以$∠DON=90^{\circ }-36^{\circ }=54^{\circ }$,故③正确;因为$∠AOE+∠BOF=90^{\circ }$,所以$∠MOE+∠NOF=\frac {1}{2}(∠AOE+∠BOF)=\frac {1}{2}×90^{\circ }=45^{\circ }$,所以$∠MON=90^{\circ }+45^{\circ }=135^{\circ }$,所以$\frac {∠MON}{∠AOE+∠BOF}=\frac {135^{\circ }}{90^{\circ }}=\frac {3}{2}=n$,所以 n 的倒数是$\frac {2}{3}$,故④正确。所以正确的说法有③④,共 2 个。
2. 如图,直线 AB,CD 相交于点 O,OF 平分∠BOD,OE 平分∠COF,∠AOD : ∠BOF = 4 : 1,则∠AOE 的度数是
$135^{\circ }$
。答案:2. $135^{\circ }$ 点拨:因为 OF 平分$∠BOD$,所以$∠BOD=2∠BOF$,$∠BOF=∠DOF$。因为$∠AOD:∠BOF=4:1$,所以$∠AOD:∠BOD=4:2$。因为$∠AOD+∠BOD=180^{\circ }$,所以$∠AOD=120^{\circ }$,$∠BOD=60^{\circ }$,所以$∠AOC=∠BOD=60^{\circ }$,$∠BOF=∠DOF=\frac {1}{2}×60^{\circ }=30^{\circ }$,所以$∠COF=180^{\circ }-∠DOF=150^{\circ }$。因为 OE 平分$∠COF$,所以$∠COE=\frac {1}{2}∠COF=\frac {1}{2}×150^{\circ }=75^{\circ }$,所以$∠AOE=∠AOC+∠COE=60^{\circ }+75^{\circ }=135^{\circ }$。
解析:
解:因为 OF 平分∠BOD,所以∠BOD=2∠BOF,∠BOF=∠DOF。
因为∠AOD:∠BOF=4:1,所以∠AOD:∠BOD=4:2。
因为∠AOD+∠BOD=180°,所以∠AOD=120°,∠BOD=60°。
所以∠AOC=∠BOD=60°,∠BOF=∠DOF=1/2×60°=30°。
所以∠COF=180°-∠DOF=150°。
因为 OE 平分∠COF,所以∠COE=1/2∠COF=1/2×150°=75°。
所以∠AOE=∠AOC+∠COE=60°+75°=135°。
故∠AOE 的度数是 135°。
因为∠AOD:∠BOF=4:1,所以∠AOD:∠BOD=4:2。
因为∠AOD+∠BOD=180°,所以∠AOD=120°,∠BOD=60°。
所以∠AOC=∠BOD=60°,∠BOF=∠DOF=1/2×60°=30°。
所以∠COF=180°-∠DOF=150°。
因为 OE 平分∠COF,所以∠COE=1/2∠COF=1/2×150°=75°。
所以∠AOE=∠AOC+∠COE=60°+75°=135°。
故∠AOE 的度数是 135°。
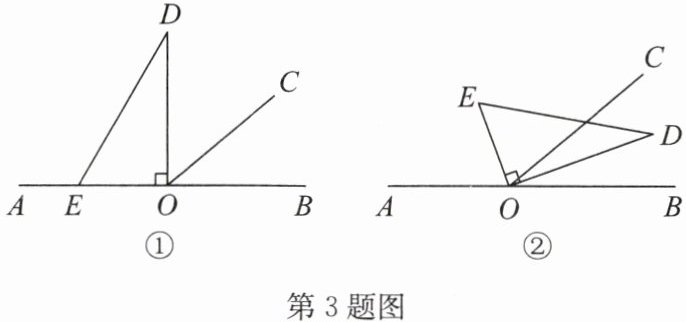
3. 以直线 AB 上一点 O 为端点作射线 OC,使∠BOC = $40^{\circ}$,将一个直角三角尺的直角顶点放在点 O 处,即∠DOE = $90^{\circ}$。
(1)如图①,若直角三角尺 DOE 的一边 OE 放在射线 OA 上,则∠COD = ______。
(2)如图②,将直角三角尺 DOE 绕点 O 顺时针转动到某个位置。
①若 OE 恰好平分∠AOC,则∠COD = ______;
②若 OD 在∠BOC 内部,请直接写出∠BOD 与∠COE 之间的数量关系。
(3)将直角三角尺 DOE 绕点 O 顺时针转动(OD 与 OB 重合时即停止)的过程中,恰好有∠COD = $\frac{1}{3}$∠AOE,求此时∠BOD 的度数。
(1)如图①,若直角三角尺 DOE 的一边 OE 放在射线 OA 上,则∠COD = ______。
(2)如图②,将直角三角尺 DOE 绕点 O 顺时针转动到某个位置。
①若 OE 恰好平分∠AOC,则∠COD = ______;
②若 OD 在∠BOC 内部,请直接写出∠BOD 与∠COE 之间的数量关系。
(3)将直角三角尺 DOE 绕点 O 顺时针转动(OD 与 OB 重合时即停止)的过程中,恰好有∠COD = $\frac{1}{3}$∠AOE,求此时∠BOD 的度数。

答案:
3. (1)$50^{\circ }$
(2)①$20^{\circ }$
②解:因为$∠COD=∠BOC - ∠BOD$,$∠COD+∠COE=90^{\circ }$,所以$∠BOC - ∠BOD+∠COE=90^{\circ }$,所以$∠COE - ∠BOD=90^{\circ }-∠BOC$。因为$∠BOC=40^{\circ }$,所以$∠COE - ∠BOD=90^{\circ }-40^{\circ }=50^{\circ }$,即$∠BOD$与$∠COE$之间的数量关系为$∠COE - ∠BOD=50^{\circ }$。
(3)解:①当$∠COD$在$∠BOC$的内部时,如答图①,
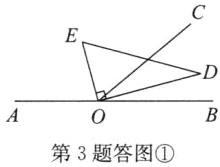
因为$∠COD=∠BOC - ∠BOD$,而$∠BOC=40^{\circ }$,所以$∠COD=40^{\circ }-∠BOD$。因为$∠AOE+∠EOD+∠BOD=180^{\circ }$,$∠EOD=90^{\circ }$,所以$∠AOE=90^{\circ }-∠BOD$。又因为$∠COD=\frac {1}{3}∠AOE$,所以$40^{\circ }-∠BOD=\frac {1}{3}(90^{\circ }-∠BOD)$,解得$∠BOD=15^{\circ }$;
②当$∠COD$在$∠BOC$的外部时,如答图②,
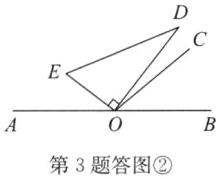
因为$∠COD=∠BOD - ∠BOC$,而$∠BOC=40^{\circ }$,所以$∠COD=∠BOD - 40^{\circ }$。因为$∠AOE+∠EOD+∠BOD=180^{\circ }$,$∠EOD=90^{\circ }$,所以$∠AOE=90^{\circ }-∠BOD$。又因为$∠COD=\frac {1}{3}∠AOE$,所以$∠BOD - 40^{\circ }=\frac {1}{3}(90^{\circ }-∠BOD)$,解得$∠BOD=52.5^{\circ }$。综上所述,$∠BOD$的度数为$15^{\circ }$或$52.5^{\circ }$。
3. (1)$50^{\circ }$
(2)①$20^{\circ }$
②解:因为$∠COD=∠BOC - ∠BOD$,$∠COD+∠COE=90^{\circ }$,所以$∠BOC - ∠BOD+∠COE=90^{\circ }$,所以$∠COE - ∠BOD=90^{\circ }-∠BOC$。因为$∠BOC=40^{\circ }$,所以$∠COE - ∠BOD=90^{\circ }-40^{\circ }=50^{\circ }$,即$∠BOD$与$∠COE$之间的数量关系为$∠COE - ∠BOD=50^{\circ }$。
(3)解:①当$∠COD$在$∠BOC$的内部时,如答图①,

因为$∠COD=∠BOC - ∠BOD$,而$∠BOC=40^{\circ }$,所以$∠COD=40^{\circ }-∠BOD$。因为$∠AOE+∠EOD+∠BOD=180^{\circ }$,$∠EOD=90^{\circ }$,所以$∠AOE=90^{\circ }-∠BOD$。又因为$∠COD=\frac {1}{3}∠AOE$,所以$40^{\circ }-∠BOD=\frac {1}{3}(90^{\circ }-∠BOD)$,解得$∠BOD=15^{\circ }$;
②当$∠COD$在$∠BOC$的外部时,如答图②,

因为$∠COD=∠BOD - ∠BOC$,而$∠BOC=40^{\circ }$,所以$∠COD=∠BOD - 40^{\circ }$。因为$∠AOE+∠EOD+∠BOD=180^{\circ }$,$∠EOD=90^{\circ }$,所以$∠AOE=90^{\circ }-∠BOD$。又因为$∠COD=\frac {1}{3}∠AOE$,所以$∠BOD - 40^{\circ }=\frac {1}{3}(90^{\circ }-∠BOD)$,解得$∠BOD=52.5^{\circ }$。综上所述,$∠BOD$的度数为$15^{\circ }$或$52.5^{\circ }$。