1. 如图,直线 AB 和 CD 相交于点 O,$OE\perp CD$,$\angle EOF = 142^{\circ}$,$\angle BOD:\angle BOF = 1:3$,则$\angle AOF$的度数为
$102^{\circ}$
。答案:$102^{\circ}$ 点拨:因为 $OE \perp CD$,所以 $\angle EOD = 90^{\circ}$.
因为 $\angle EOF = 142^{\circ}$,所以 $\angle DOF = 142^{\circ} - 90^{\circ} = 52^{\circ}$.
因为 $\angle BOD:\angle BOF = 1:3$,所以 $\angle BOD = \frac{1}{2}\angle DOF = 26^{\circ}$,
所以 $\angle BOF = \angle BOD + \angle DOF = 78^{\circ}$.
因为 $\angle AOF + \angle BOF = 180^{\circ}$,
所以 $\angle AOF = 180^{\circ} - \angle BOF = 180^{\circ} - 78^{\circ} = 102^{\circ}$.
因为 $\angle EOF = 142^{\circ}$,所以 $\angle DOF = 142^{\circ} - 90^{\circ} = 52^{\circ}$.
因为 $\angle BOD:\angle BOF = 1:3$,所以 $\angle BOD = \frac{1}{2}\angle DOF = 26^{\circ}$,
所以 $\angle BOF = \angle BOD + \angle DOF = 78^{\circ}$.
因为 $\angle AOF + \angle BOF = 180^{\circ}$,
所以 $\angle AOF = 180^{\circ} - \angle BOF = 180^{\circ} - 78^{\circ} = 102^{\circ}$.
2. 已知直线 AB 与直线 CD 相交于点 O,过点 O 作$OE\perp CD$。
(1) 如图①,若$\angle AOE = 2\angle AOC$,求$\angle BOE$的度数;
(2) 如图②,过点 O 画直线 FG,满足射线 OF 在$\angle EOD$内部,且使$\angle AOC = 2\angle EOF$,在不添加任何辅助线的情况下,请直接写出与$\angle EOF$互余的角。
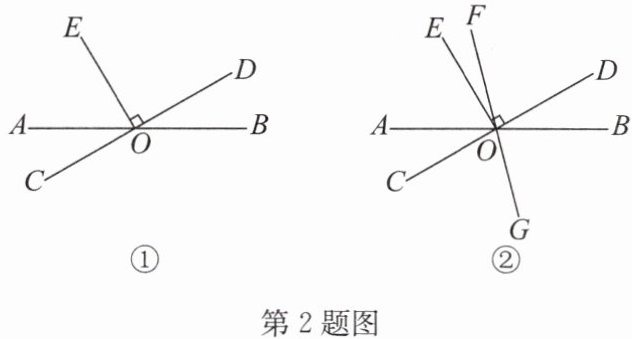
(1) 如图①,若$\angle AOE = 2\angle AOC$,求$\angle BOE$的度数;
(2) 如图②,过点 O 画直线 FG,满足射线 OF 在$\angle EOD$内部,且使$\angle AOC = 2\angle EOF$,在不添加任何辅助线的情况下,请直接写出与$\angle EOF$互余的角。

答案:解:(1)因为 $OE \perp CD$,
所以 $\angle COE = \angle DOE = 90^{\circ}$,
所以 $\angle AOC + \angle AOE = 90^{\circ}$.
因为 $\angle AOE = 2\angle AOC$,
所以 $\angle AOC + 2\angle AOC = 90^{\circ}$,解得 $\angle AOC = 30^{\circ}$,
所以 $\angle BOD = \angle AOC = 30^{\circ}$,
所以 $\angle BOE = \angle BOD + \angle DOE = 30^{\circ} + 90^{\circ} = 120^{\circ}$.
(2)因为 $OE \perp CD$,所以 $\angle DOE = 90^{\circ}$,
所以 $\angle DOF + \angle EOF = 90^{\circ}$.
因为 $\angle COG = \angle DOF$,所以 $\angle COG + \angle EOF = 90^{\circ}$.
因为 $\angle AOE + \angle AOC = 90^{\circ}, \angle AOC = 2\angle EOF$,
所以 $\angle AOE + 2\angle EOF = 90^{\circ}$,
$所以∠AOF+∠EOF=90°$
$因为∠BOG=∠AOF$
$所以∠BOG+∠EOF=90°$
$所以∠EOF互余的角有∠FOD,∠COG,∠BOG,∠AOF$
所以 $\angle COE = \angle DOE = 90^{\circ}$,
所以 $\angle AOC + \angle AOE = 90^{\circ}$.
因为 $\angle AOE = 2\angle AOC$,
所以 $\angle AOC + 2\angle AOC = 90^{\circ}$,解得 $\angle AOC = 30^{\circ}$,
所以 $\angle BOD = \angle AOC = 30^{\circ}$,
所以 $\angle BOE = \angle BOD + \angle DOE = 30^{\circ} + 90^{\circ} = 120^{\circ}$.
(2)因为 $OE \perp CD$,所以 $\angle DOE = 90^{\circ}$,
所以 $\angle DOF + \angle EOF = 90^{\circ}$.
因为 $\angle COG = \angle DOF$,所以 $\angle COG + \angle EOF = 90^{\circ}$.
因为 $\angle AOE + \angle AOC = 90^{\circ}, \angle AOC = 2\angle EOF$,
所以 $\angle AOE + 2\angle EOF = 90^{\circ}$,
$所以∠AOF+∠EOF=90°$
$因为∠BOG=∠AOF$
$所以∠BOG+∠EOF=90°$
$所以∠EOF互余的角有∠FOD,∠COG,∠BOG,∠AOF$