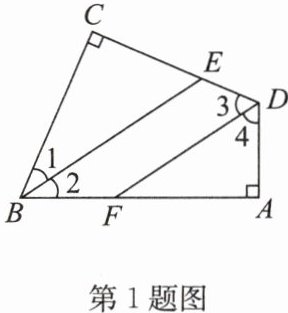
1. 如图, 在四边形 $ABCD$ 中, $\angle A= \angle C = 90^{\circ}$, $BE$ 平分 $\angle ABC$, $DF$ 平分 $\angle ADC$, 则 $BE$ 与 $DF$ 有何位置关系? 试说明理由.

答案:解:$BE// DF$. 理由如下:
因为$∠A=∠C=90^{\circ }$(已知),
所以$∠ABC+∠ADC=180^{\circ }$.
因为$BE$平分$∠ABC$,$DF$平分$∠ADC$,
所以$∠1=∠2=\frac {1}{2}∠ABC$,$∠3=∠4=\frac {1}{2}∠ADC$(角平分线的定义),
所以$∠1+∠3=\frac {1}{2}(∠ABC+∠ADC)=\frac {1}{2}×180^{\circ }=90^{\circ }$(等式的性质).
又$∠1+∠CEB=90^{\circ }$,
所以$∠3=∠CEB$(同角的余角相等),
所以$BE// DF$(同位角相等,两直线平行).
因为$∠A=∠C=90^{\circ }$(已知),
所以$∠ABC+∠ADC=180^{\circ }$.
因为$BE$平分$∠ABC$,$DF$平分$∠ADC$,
所以$∠1=∠2=\frac {1}{2}∠ABC$,$∠3=∠4=\frac {1}{2}∠ADC$(角平分线的定义),
所以$∠1+∠3=\frac {1}{2}(∠ABC+∠ADC)=\frac {1}{2}×180^{\circ }=90^{\circ }$(等式的性质).
又$∠1+∠CEB=90^{\circ }$,
所以$∠3=∠CEB$(同角的余角相等),
所以$BE// DF$(同位角相等,两直线平行).
2. 如图, 点 $E,F$ 分别在 $AB,CD$ 上, $AF\perp CE$, 垂足为 $O$, $\angle 1= \angle B$, $\angle A+\angle 2 = 90^{\circ}$. 试说明: $AB// CD$.


答案:解:因为$∠1=∠B$(已知),
所以$CE// BF$(同位角相等,两直线平行),
所以$∠AOE=∠AFB$(两直线平行,同位角相等).
因为$AF⊥CE$(已知),
所以$∠AOE=90^{\circ }$(垂直的定义),
所以$∠AFB=90^{\circ }$(等量代换).
因为$∠AFC+∠AFB+∠2=180^{\circ }$(平角的定义),
所以$∠AFC+∠2=90^{\circ }$(等式的性质),
因为$∠A+∠2=90^{\circ }$(已知),
所以$∠AFC=∠A$(同角的余角相等),
所以$AB// CD$(内错角相等,两直线平行).
所以$CE// BF$(同位角相等,两直线平行),
所以$∠AOE=∠AFB$(两直线平行,同位角相等).
因为$AF⊥CE$(已知),
所以$∠AOE=90^{\circ }$(垂直的定义),
所以$∠AFB=90^{\circ }$(等量代换).
因为$∠AFC+∠AFB+∠2=180^{\circ }$(平角的定义),
所以$∠AFC+∠2=90^{\circ }$(等式的性质),
因为$∠A+∠2=90^{\circ }$(已知),
所以$∠AFC=∠A$(同角的余角相等),
所以$AB// CD$(内错角相等,两直线平行).