1. 如图,直线 $ AB // CD $,两相交直线 $ EF $, $ GH $ 与 $ AB $, $ CD $ 都相交,图中的同旁内角共有 (
A.4 对
B.8 对
C.12 对
D.16 对
D
)A.4 对
B.8 对
C.12 对
D.16 对
答案:D 点拨:直线AB,CD被EF所截有2对同旁内角;
直线AB,CD被GH所截有2对同旁内角;
直线CD,EF被GH所截有2对同旁内角;
直线CD,GH被EF所截有2对同旁内角;
直线AB,EF被GH所截有2对同旁内角;
直线AB,GH被EF所截有2对同旁内角;
直线GH,EF被CD所截有2对同旁内角;
直线EF,GH被AB所截有2对同旁内角.
共有16对同旁内角.
直线AB,CD被GH所截有2对同旁内角;
直线CD,EF被GH所截有2对同旁内角;
直线CD,GH被EF所截有2对同旁内角;
直线AB,EF被GH所截有2对同旁内角;
直线AB,GH被EF所截有2对同旁内角;
直线GH,EF被CD所截有2对同旁内角;
直线EF,GH被AB所截有2对同旁内角.
共有16对同旁内角.
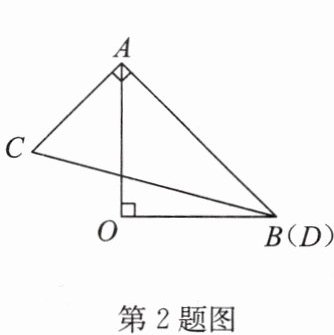
2. 一副三角尺按如图所示方式叠放在一起,其中点 $ B $, $ D $ 重合,若固定三角尺 $ AOB $,改变三角尺 $ ACD $ 的位置(其中点 $ A $ 位置始终不变).
(1) 当 $ \angle BAD = $
(2) 当 $ \angle BAD = $
(1) 当 $ \angle BAD = $
150°或30°
时, $ CD // AB $;(2) 当 $ \angle BAD = $
15°或45°或135°或165°
时,三角尺 $ ACD $ 有一条边与直角边 $ OB $ 平行. (填度数,写出所有可能的情况)
答案:(1)150°或30° 点拨:如答图①,当CD//AB时,∠BAD=∠D=30°;
如答图②,当AB//CD时,∠C=∠BAC=60°,
所以∠BAD=60°+90°=150°.
(2)15°或45°或135°或165° 点拨:如答图③,当CD//OB时,∠BAD=15°;
如答图④,当AD//BO时,∠BAD=∠B=45°;
如答图⑤,当AC//BO时,∠BAD=45°+90°=135°;
如答图⑥,当CD//BO时,∠BAD=165°;
如答图⑦,当AD//BO时,∠BAD=45°+90°=135°;
如答图⑧,当AC//BO时,∠BAD=45°.
综上所述,∠BAD的度数为15°或45°或135°或165°.
如答图②,当AB//CD时,∠C=∠BAC=60°,
所以∠BAD=60°+90°=150°.
(2)15°或45°或135°或165° 点拨:如答图③,当CD//OB时,∠BAD=15°;
如答图④,当AD//BO时,∠BAD=∠B=45°;
如答图⑤,当AC//BO时,∠BAD=45°+90°=135°;
如答图⑥,当CD//BO时,∠BAD=165°;
如答图⑦,当AD//BO时,∠BAD=45°+90°=135°;
如答图⑧,当AC//BO时,∠BAD=45°.
综上所述,∠BAD的度数为15°或45°或135°或165°.
3. 如图, $ BE \perp DE $, $ \angle 1 = \angle B $, $ \angle 2 = \angle D $,试确定 $ AB $ 与 $ CD $ 的位置关系,并说明理由.


答案:解:AB//CD.
理由:如答图,过点E作EN//AB,则∠BEN=∠B.
因为∠1=∠B,所以∠BEN=∠1.
因为BE⊥DE,所以∠BED=90°,
所以∠BEN+∠DEN=90°,∠1+∠2=90°,
所以∠2=∠DEN.
因为∠2=∠D,所以∠D=∠DEN,
所以CD//EN,所以AB//CD.
理由:如答图,过点E作EN//AB,则∠BEN=∠B.
因为∠1=∠B,所以∠BEN=∠1.
因为BE⊥DE,所以∠BED=90°,
所以∠BEN+∠DEN=90°,∠1+∠2=90°,
所以∠2=∠DEN.
因为∠2=∠D,所以∠D=∠DEN,
所以CD//EN,所以AB//CD.