1. 如图,若$AB// DE,∠B= 130^{\circ },∠D= 35^{\circ }$,则$∠C$的度数为 (
A.$80^{\circ }$
B.$85^{\circ }$
C.$90^{\circ }$
D.$95^{\circ }$
B
)A.$80^{\circ }$
B.$85^{\circ }$
C.$90^{\circ }$
D.$95^{\circ }$
答案：B
解析：
解：过点C作CF//AB，
∵AB//DE，
∴CF//DE，
∵CF//AB，∠B=130°，
∴∠BCF=180°-∠B=180°-130°=50°，
∵CF//DE，∠D=35°，
∴∠DCF=∠D=35°，
∴∠C=∠BCF+∠DCF=50°+35°=85°。
答案：B
∵AB//DE，
∴CF//DE，
∵CF//AB，∠B=130°，
∴∠BCF=180°-∠B=180°-130°=50°，
∵CF//DE，∠D=35°，
∴∠DCF=∠D=35°，
∴∠C=∠BCF+∠DCF=50°+35°=85°。
答案：B
2. 如图,$AD// BC,AB// CD$,BE 平分$∠ABC$,EC 平分$∠BED$,若$∠ECD= 45^{\circ }$,则$∠ABC$的度数为
$60^{\circ}$
.答案：$60^{\circ}$ 点拨:因为 $BE$ 平分 $\angle ABC$，$EC$ 平分 $\angle BED$，所以 $\angle CBE=\frac{1}{2}\angle ABC$，$\angle BEC=\angle CED$。因为 $AD// BC$，$AB// CD$，所以 $\angle CBE=\angle AEB=\frac{1}{2}\angle ABC$，$\angle CED=\angle BCE$，$\angle ABC+\angle BCD=180^{\circ}$。因为 $\angle AEB+\angle BED=180^{\circ}$，所以 $\angle BED=180^{\circ}-\angle AEB=180^{\circ}-\frac{1}{2}\angle ABC$，所以 $\angle CED=\frac{1}{2}\angle BED=90^{\circ}-\frac{1}{4}\angle ABC$，所以 $\angle BCE=90^{\circ}-\frac{1}{4}\angle ABC$。因为 $\angle ABC+\angle BCD=180^{\circ}$，所以 $\angle ABC+\angle BCE+\angle ECD=180^{\circ}$，即 $\angle ABC+90^{\circ}-\frac{1}{4}\angle ABC+45^{\circ}=180^{\circ}$，解得 $\angle ABC=60^{\circ}$。
解析：
解：因为BE平分∠ABC，EC平分∠BED，
所以∠CBE=1/2∠ABC，∠BEC=∠CED。
因为AD//BC，AB//CD，
所以∠CBE=∠AEB=1/2∠ABC，∠CED=∠BCE，∠ABC+∠BCD=180°。
因为∠AEB+∠BED=180°，
所以∠BED=180°-∠AEB=180°-1/2∠ABC，
所以∠CED=1/2∠BED=90°-1/4∠ABC，
所以∠BCE=90°-1/4∠ABC。
因为∠ABC+∠BCD=180°，∠BCD=∠BCE+∠ECD，∠ECD=45°，
所以∠ABC+∠BCE+45°=180°，
即∠ABC+90°-1/4∠ABC+45°=180°，
解得∠ABC=60°。
60°
所以∠CBE=1/2∠ABC，∠BEC=∠CED。
因为AD//BC，AB//CD，
所以∠CBE=∠AEB=1/2∠ABC，∠CED=∠BCE，∠ABC+∠BCD=180°。
因为∠AEB+∠BED=180°，
所以∠BED=180°-∠AEB=180°-1/2∠ABC，
所以∠CED=1/2∠BED=90°-1/4∠ABC，
所以∠BCE=90°-1/4∠ABC。
因为∠ABC+∠BCD=180°，∠BCD=∠BCE+∠ECD，∠ECD=45°，
所以∠ABC+∠BCE+45°=180°，
即∠ABC+90°-1/4∠ABC+45°=180°，
解得∠ABC=60°。
60°
3. 如图,点 C,D 分别在射线 OA,OB 上,不与点 O 重合,且$CE// DF.$
(1) 如图①,探究$∠ACE,∠AOB,∠ODF$的数量关系,并说明理由;
(2) 如图②,作$CP⊥OA$,与$∠ODF$的平分线交于点 P,若$∠ACE= α,∠AOB= β$,请用含 α,β 的式子表示$∠P= $______.(直接写出结果)
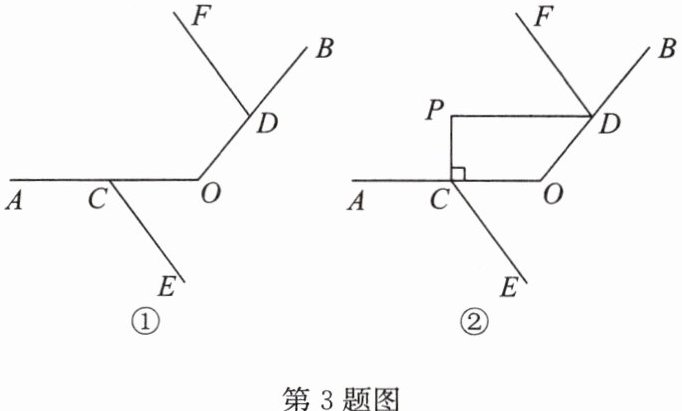
(1) 如图①,探究$∠ACE,∠AOB,∠ODF$的数量关系,并说明理由;
(2) 如图②,作$CP⊥OA$,与$∠ODF$的平分线交于点 P,若$∠ACE= α,∠AOB= β$,请用含 α,β 的式子表示$∠P= $______.(直接写出结果)
答案：
(1) 解: $\angle ODF+\angle AOB+\angle ACE=360^{\circ}$。理由: 如答图，过点 $O$ 作直线 $OG// FD$，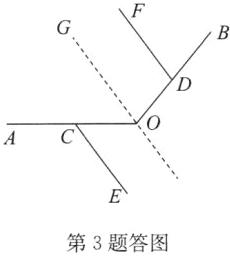
所以 $\angle ODF+\angle DOG=180^{\circ}$。又因为 $OG// FD$，$CE// DF$，所以 $OG// CE$，所以 $\angle GOC=\angle OCE$。又因为 $\angle ACE+\angle OCE=180^{\circ}$，所以 $\angle ACE+\angle GOC=180^{\circ}$，所以 $\angle ODF+\angle DOG+\angle ACE+\angle GOC=360^{\circ}$，即 $\angle ODF+\angle AOB+\angle ACE=360^{\circ}$。
(2) $90^{\circ}+\frac{1}{2}\alpha-\frac{1}{2}\beta$ 点拨: 因为 $DP$ 是 $\angle ODF$ 的平分线，所以 $\angle ODP=\frac{1}{2}\angle ODF$，所以 $\angle P=360^{\circ}-\angle PCO-\beta-\angle ODP=360^{\circ}-90^{\circ}-\beta-\frac{1}{2}\angle ODF=270^{\circ}-\beta-\frac{1}{2}(360^{\circ}-\alpha-\beta)=90^{\circ}+\frac{1}{2}\alpha-\frac{1}{2}\beta$。
(1) 解: $\angle ODF+\angle AOB+\angle ACE=360^{\circ}$。理由: 如答图，过点 $O$ 作直线 $OG// FD$，
所以 $\angle ODF+\angle DOG=180^{\circ}$。又因为 $OG// FD$，$CE// DF$，所以 $OG// CE$，所以 $\angle GOC=\angle OCE$。又因为 $\angle ACE+\angle OCE=180^{\circ}$，所以 $\angle ACE+\angle GOC=180^{\circ}$，所以 $\angle ODF+\angle DOG+\angle ACE+\angle GOC=360^{\circ}$，即 $\angle ODF+\angle AOB+\angle ACE=360^{\circ}$。(2) $90^{\circ}+\frac{1}{2}\alpha-\frac{1}{2}\beta$ 点拨: 因为 $DP$ 是 $\angle ODF$ 的平分线，所以 $\angle ODP=\frac{1}{2}\angle ODF$，所以 $\angle P=360^{\circ}-\angle PCO-\beta-\angle ODP=360^{\circ}-90^{\circ}-\beta-\frac{1}{2}\angle ODF=270^{\circ}-\beta-\frac{1}{2}(360^{\circ}-\alpha-\beta)=90^{\circ}+\frac{1}{2}\alpha-\frac{1}{2}\beta$。