1. 若$-x= 2$,则$-[-(-x)]= $
2
.答案:2
解析:
解:因为 $-x = 2$,所以 $-[-(-x)] = -x = 2$。
2
2
2. 已知$m与n$互为相反数,且$m与n$之间的距离为6,$m < n$,则$m= $
$-3$
,$n= $$3$
.答案:$-3$
解析:
解:因为$m$与$n$互为相反数,所以$n = -m$。
又因为$m$与$n$之间的距离为$6$,且$m < n$,所以$n - m = 6$。
将$n = -m$代入$n - m = 6$,得$-m - m = 6$,即$-2m = 6$,解得$m = -3$。
则$n = -m = -(-3) = 3$。
$m = -3$,$n = 3$
又因为$m$与$n$之间的距离为$6$,且$m < n$,所以$n - m = 6$。
将$n = -m$代入$n - m = 6$,得$-m - m = 6$,即$-2m = 6$,解得$m = -3$。
则$n = -m = -(-3) = 3$。
$m = -3$,$n = 3$
3. 已知数轴上点$A表示的数是+8$,$B$,$C$两点表示的数互为相反数,且点$C到点A$的距离为3,点$B和点C$分别表示什么数?
答案:解:当点C在点A的左侧时,$8 - 3 = 5$,此时点B表示的数是$-5$;
当点C在点A的右侧时,$8 + 3 = 11$,此时点B表示的数是$-11$。
综上可知,点B和点C分别表示$-5$,5或$-11$,11。
当点C在点A的右侧时,$8 + 3 = 11$,此时点B表示的数是$-11$。
综上可知,点B和点C分别表示$-5$,5或$-11$,11。
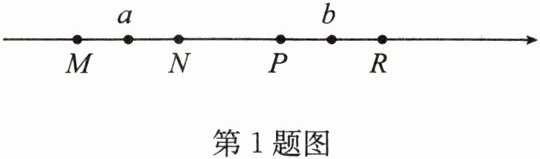
1. 如图,M,N,P,R分别是数轴上四个连续整数所对应的点,其中有一个点是原点。数a对应的点在M与N之间,数b对应的点在P与R之间,$|a|+|b|= 3$,则原点是(
A.M或R
B.N或P
C.M或N
D.P或R
A
)
A.M或R
B.N或P
C.M或N
D.P或R
答案:A 点拨:由题图知a,b两个数之间的距离小于3,又$|a|+|b|=3$,所以原点不在a,b两个数之间,即原点不是N或P,所以原点是M或R.
2. 已知$-a < b < -c < 0 < -d$,且$|d| < |c|$,试将a,b,c,d,0按从大到小的顺序排列,并在数轴上画出表示a,b,c,d的点。
答案:
解:因为$-a\lt b<-c<0<-d$,所以$a>0,b<0,c>0,d<0,|-a|>|b|>|-c|$.又因为$|-a|=|a|,|-c|=|c|,|d|<|c|$,所以$|a|>|b|>|c|>|d|$,所以$a>c>0>d>b$.将它们在数轴上表示出来如答图,

解:因为$-a\lt b<-c<0<-d$,所以$a>0,b<0,c>0,d<0,|-a|>|b|>|-c|$.又因为$|-a|=|a|,|-c|=|c|,|d|<|c|$,所以$|a|>|b|>|c|>|d|$,所以$a>c>0>d>b$.将它们在数轴上表示出来如答图,
