1.(2024·江阴月考)当$a= 2,b= -3$时,代数式$(a-b)^{2}+2ab$的值为 (
A.13
B.27
C.-5
D.-7
A
)A.13
B.27
C.-5
D.-7
答案:A
解析:
解:将$a = 2$,$b=-3$代入代数式$(a - b)^2+2ab$,得
$\begin{aligned}&(2 - (-3))^2+2×2×(-3)\\=&(2 + 3)^2+(-12)\\=&5^2-12\\=&25-12\\=&13\end{aligned}$
答案:A
$\begin{aligned}&(2 - (-3))^2+2×2×(-3)\\=&(2 + 3)^2+(-12)\\=&5^2-12\\=&25-12\\=&13\end{aligned}$
答案:A
2.按如图所示的运算程序,能使运算输出的结果为7的是 (
A.$x= -2,y= 3$
B.$x= -2,y= -3$
C.$x= 8,y= -3$
D.$x= -8,y= 3$
C
)A.$x= -2,y= 3$
B.$x= -2,y= -3$
C.$x= 8,y= -3$
D.$x= -8,y= 3$
答案:C
解析:
解:
A. $x=-2 \leq 0$,输出 $2×(-2)+3^2=-4+9=5\neq7$
B. $x=-2 \leq 0$,输出 $2×(-2)+(-3)^2=-4+9=5\neq7$
C. $x=8 > 0$,输出 $2×8-(-3)^2=16-9=7$
D. $x=-8 \leq 0$,输出 $2×(-8)+3^2=-16+9=-7\neq7$
结论:C
A. $x=-2 \leq 0$,输出 $2×(-2)+3^2=-4+9=5\neq7$
B. $x=-2 \leq 0$,输出 $2×(-2)+(-3)^2=-4+9=5\neq7$
C. $x=8 > 0$,输出 $2×8-(-3)^2=16-9=7$
D. $x=-8 \leq 0$,输出 $2×(-8)+3^2=-16+9=-7\neq7$
结论:C
3.(2024·姜堰区一模)若$2a-b= 3$,则$4a-2b+1= $
7
.答案:7
解析:
解:因为$2a - b = 3$,所以$4a - 2b = 2(2a - b) = 2×3 = 6$,则$4a - 2b + 1 = 6 + 1 = 7$。
7
7
4.(2024·金坛区期中)按如图所示的程序计算,若输入的数值为3,则输出的结果是
$-\frac{1}{2}$
.答案:$-\frac{1}{2}$
解析:
输入3:
第一步:$3 - 6 = -3$
第二步:$-3 + (-2)^2 = -3 + 4 = 1$
第三步:$1 ÷ (-2) = -\frac{1}{2}$
判断:$-\frac{1}{2} > -1$,是
输出:$-\frac{1}{2}$
$-\frac{1}{2}$
第一步:$3 - 6 = -3$
第二步:$-3 + (-2)^2 = -3 + 4 = 1$
第三步:$1 ÷ (-2) = -\frac{1}{2}$
判断:$-\frac{1}{2} > -1$,是
输出:$-\frac{1}{2}$
$-\frac{1}{2}$
5.已知$a,b$互为相反数,$c,d$互为倒数,那么$a+b-cd= $
-1
.答案:-1
解析:
解:因为$a$,$b$互为相反数,所以$a + b=0$;
因为$c$,$d$互为倒数,所以$cd = 1$;
则$a + b-cd=0 - 1=-1$。
$-1$
因为$c$,$d$互为倒数,所以$cd = 1$;
则$a + b-cd=0 - 1=-1$。
$-1$
6.先填表,再回答问题:

(1)当$x$为何值时,代数式$2x-1$的值等于5?
(2)已知有一个$x的值使代数式-x+5和2x-1$的值相等,你能找出这个$x$的值吗?
(3)随着$x$值的逐渐增大,代数式$-x+5,2x-1$的值是如何变化的?(写出结论即可,无须说明理由)

(1)当$x$为何值时,代数式$2x-1$的值等于5?
(2)已知有一个$x的值使代数式-x+5和2x-1$的值相等,你能找出这个$x$的值吗?
(3)随着$x$值的逐渐增大,代数式$-x+5,2x-1$的值是如何变化的?(写出结论即可,无须说明理由)
答案:
解:填表如下.
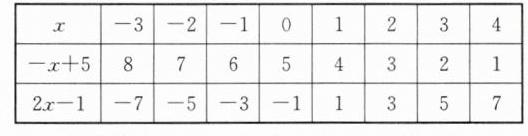
(1) 根据表格,得当 $x = 3$ 时,代数式 $2x - 1$ 的值等于 5.
(2) 当 $x = 2$ 时,代数式 $-x + 5$ 和 $2x - 1$ 的值相等.
(3) 代数式 $-x + 5$ 的值随 $x$ 值的增大而减小;代数式 $2x - 1$ 的值随 $x$ 值的增大而增大.
解:填表如下.

(1) 根据表格,得当 $x = 3$ 时,代数式 $2x - 1$ 的值等于 5.
(2) 当 $x = 2$ 时,代数式 $-x + 5$ 和 $2x - 1$ 的值相等.
(3) 代数式 $-x + 5$ 的值随 $x$ 值的增大而减小;代数式 $2x - 1$ 的值随 $x$ 值的增大而增大.
7.如图,一个十字形花坛铺上了草皮,四个角没有种草的部分都是正方形.
(1)此花坛草地的面积可以用代数式表示为
(2)若$a= 12$米,$b= 8$米,$c= 2$米,则此花坛草地的面积是多少平方米?

(1)此花坛草地的面积可以用代数式表示为
$ab - 4c^2$
;(2)若$a= 12$米,$b= 8$米,$c= 2$米,则此花坛草地的面积是多少平方米?

80 平方米
答案:(1) $ab - 4c^2$ (2) 80 平方米
解析:
(1) $ab - 4c^2$
(2) 解:当$a = 12$米,$b = 8$米,$c = 2$米时,
$ab - 4c^2 = 12×8 - 4×2^2$
$= 96 - 4×4$
$= 96 - 16$
$= 80$
答:此花坛草地的面积是80平方米。
(2) 解:当$a = 12$米,$b = 8$米,$c = 2$米时,
$ab - 4c^2 = 12×8 - 4×2^2$
$= 96 - 4×4$
$= 96 - 16$
$= 80$
答:此花坛草地的面积是80平方米。