1. 单项式中的
数字因数
叫作单项式的系数;单项式中所有字母的指数的和
叫作单项式的次数。答案:数字因数 指数的和
2. 几个单项式的
和
的代数式叫作多项式;多项式中,每个单项式
叫作多项式的项;其中次数最高的项的次数
叫作这个多项式的次数,不含字母的项叫作常数项
。答案:和 单项式 次数最高的项的次数 常数项
3.
单项式
和多项式
统称整式。答案:单项式 多项式
1. 单项式$-\frac {2^{3}xy^{4}}{7}$的次数是 (
A.8
B.3
C.4
D.5
D
)A.8
B.3
C.4
D.5
答案:D
解析:
解:单项式的次数是所有字母的指数和。在单项式$-\frac{2^{3}xy^{4}}{7}$中,$x$的指数是$1$,$y$的指数是$4$,所以次数为$1 + 4 = 5$。
答案:D
答案:D
2. 多项式$m^{3}n^{4}-5m^{3}n^{5}+3$的项数和次数分别为 (
A.2,7
B.3,8
C.2,8
D.3,7
B
)A.2,7
B.3,8
C.2,8
D.3,7
答案:B
解析:
多项式$m^{3}n^{4}-5m^{3}n^{5}+3$由$m^{3}n^{4}$、$-5m^{3}n^{5}$、$3$三项组成,故项数为3。
各项次数:$m^{3}n^{4}$的次数为$3 + 4 = 7$;$-5m^{3}n^{5}$的次数为$3 + 5 = 8$;常数项$3$的次数为0。
该多项式的次数为各项次数中的最高次,即8。
综上,项数为3,次数为8,答案选B。
各项次数:$m^{3}n^{4}$的次数为$3 + 4 = 7$;$-5m^{3}n^{5}$的次数为$3 + 5 = 8$;常数项$3$的次数为0。
该多项式的次数为各项次数中的最高次,即8。
综上,项数为3,次数为8,答案选B。
3. (2024·徐州期末)对于多项式$-2x^{2}+5x-3$,下列说法正确的是 (
A.它是三次三项式
B.它的常数项是 3
C.它的一次项系数是 5
D.它的二次项系数是 2
C
)A.它是三次三项式
B.它的常数项是 3
C.它的一次项系数是 5
D.它的二次项系数是 2
答案:C
解析:
解:多项式$-2x^{2}+5x - 3$的项分别为$-2x^{2}$、$5x$、$-3$。
最高次项是$-2x^{2}$,次数为2,所以是二次三项式,A错误;
常数项是$-3$,B错误;
一次项是$5x$,系数是5,C正确;
二次项是$-2x^{2}$,系数是$-2$,D错误。
答案:C
最高次项是$-2x^{2}$,次数为2,所以是二次三项式,A错误;
常数项是$-3$,B错误;
一次项是$5x$,系数是5,C正确;
二次项是$-2x^{2}$,系数是$-2$,D错误。
答案:C
4. $-5^{2}π^{2}a^{4}b$是单项式,它的系数和次数分别是 (
A.系数是-5,次数是 9
B.系数是$5^{2}$,次数是 7
C.系数是$-5^{2}$,次数是 7
D.系数是$-5^{2}π^{2}$,次数是 5
D
)A.系数是-5,次数是 9
B.系数是$5^{2}$,次数是 7
C.系数是$-5^{2}$,次数是 7
D.系数是$-5^{2}π^{2}$,次数是 5
答案:D
解析:
解:对于单项式$-5^{2}π^{2}a^{4}b$,
系数是指单项式中的数字因数,包括前面的符号及所有常数项,所以系数为$-5^{2}π^{2}$;
次数是指单项式中所有字母的指数和,字母$a$的指数是$4$,字母$b$的指数是$1$,故次数为$4 + 1=5$。
答案:D
系数是指单项式中的数字因数,包括前面的符号及所有常数项,所以系数为$-5^{2}π^{2}$;
次数是指单项式中所有字母的指数和,字母$a$的指数是$4$,字母$b$的指数是$1$,故次数为$4 + 1=5$。
答案:D
5. 小雨写了几个多项式,其中是五次三项式的是 (
A.$y^{5}-1$
B.$5x^{2}y^{2}-x+y$
C.$3a^{2}b^{2}c-ab+1$
D.$3a^{5}b-b+c$
C
)A.$y^{5}-1$
B.$5x^{2}y^{2}-x+y$
C.$3a^{2}b^{2}c-ab+1$
D.$3a^{5}b-b+c$
答案:C
解析:
解:A. $y^5 - 1$ 是五次二项式;
B. $5x^2y^2 - x + y$ 是四次三项式;
C. $3a^2b^2c - ab + 1$ 是五次三项式;
D. $3a^5b - b + c$ 是六次三项式。
答案:C
B. $5x^2y^2 - x + y$ 是四次三项式;
C. $3a^2b^2c - ab + 1$ 是五次三项式;
D. $3a^5b - b + c$ 是六次三项式。
答案:C
6. 下列说法正确的是 (
A.$-3^{3}a^{2}bc^{2}$的系数为-3,次数为 27
B.$\frac {x}{π}+\frac {y}{2}+\frac {z^{2}}{3}$不是单项式,但是整式
C.$\frac {1}{x+1}$是多项式
D.$mx^{2}+1$一定是关于 x 的二次二项式
B
)A.$-3^{3}a^{2}bc^{2}$的系数为-3,次数为 27
B.$\frac {x}{π}+\frac {y}{2}+\frac {z^{2}}{3}$不是单项式,但是整式
C.$\frac {1}{x+1}$是多项式
D.$mx^{2}+1$一定是关于 x 的二次二项式
答案:B
解析:
解:
A. $-3^{3}a^{2}bc^{2}$的系数为$-27$,次数为$5$,故A错误;
B. $\frac{x}{\pi}+\frac{y}{2}+\frac{z^{2}}{3}$是多项式,不是单项式,是整式,故B正确;
C. $\frac{1}{x+1}$是分式,不是多项式,故C错误;
D. 当$m=0$时,$mx^{2}+1$是常数项,不是二次二项式,故D错误。
答案:B
A. $-3^{3}a^{2}bc^{2}$的系数为$-27$,次数为$5$,故A错误;
B. $\frac{x}{\pi}+\frac{y}{2}+\frac{z^{2}}{3}$是多项式,不是单项式,是整式,故B正确;
C. $\frac{1}{x+1}$是分式,不是多项式,故C错误;
D. 当$m=0$时,$mx^{2}+1$是常数项,不是二次二项式,故D错误。
答案:B
7. 若多项式$3x^{2}+kx-2x+1$(k 为常数)中不含有 x 的一次项,则$k=$
2
。答案:2
解析:
解:$3x^{2}+kx-2x+1=3x^{2}+(k-2)x+1$,
因为多项式中不含有$x$的一次项,
所以$k-2=0$,
解得$k=2$。
答案:$2$
因为多项式中不含有$x$的一次项,
所以$k-2=0$,
解得$k=2$。
答案:$2$
8. 将下列式子按要求分类:$2,3x,\frac {1}{x},π,4a^{2}b,5-\frac {1}{2}y,\frac {1-x}{3}$。
整式:
多项式:
整式:
$2,3x,π,4a^{2}b,5-\frac {1}{2}y,\frac {1-x}{3}$
; 单项式:$2,3x,π,4a^{2}b$
;多项式:
$5-\frac {1}{2}y,\frac {1-x}{3}$
。答案:整式:$2,3x,π,4a^{2}b,5-\frac {1}{2}y,\frac {1-x}{3}$; 单项式:$2,3x,π,4a^{2}b$;多项式:$5-\frac {1}{2}y,\frac {1-x}{3}$
9. 填表:
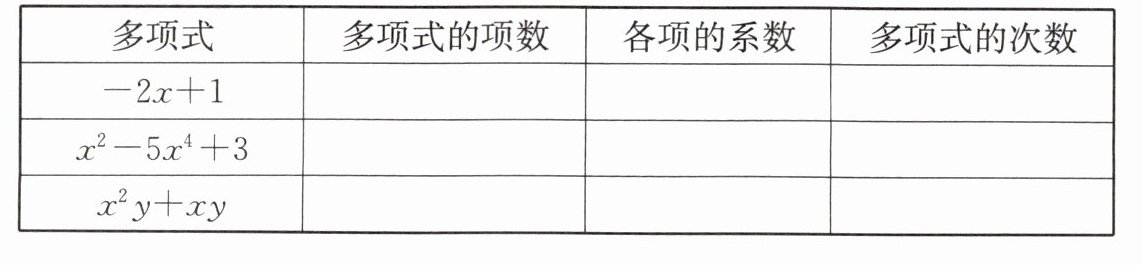

答案:
解:如下表所示:

解:如下表所示:
