1. 某口罩厂有 80 名工人,每人每天可以生产 1000 个口罩面或 1200 根耳绳. 一个口罩面需要配两根耳绳,为使每天生产的口罩面与耳绳刚好配套,应安排生产口罩面和耳绳的工人各多少名?
答案:解:设应安排 x 名工人生产口罩面,则安排$(80-x)$名工人生产耳绳,
根据题意,得$2×1000x=1200(80-x)$,
解得$x=30$,
则$80-x=80-30=50$.
答:应安排 30 名工人生产口罩面,50 名工人生产耳绳.
根据题意,得$2×1000x=1200(80-x)$,
解得$x=30$,
则$80-x=80-30=50$.
答:应安排 30 名工人生产口罩面,50 名工人生产耳绳.
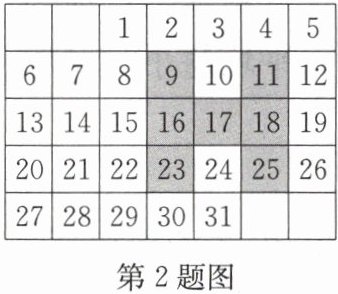
2. 如图是某年八月份的日历.
(1)若将“H”形框上下左右移动,可框住 7 个数,若设“H”形框中的 7 个数中最中间一个数是 x,请用含 x 的代数式由小到大依次表示出“H”形框中的其余 6 个数;
(2)请问“H”形框能否框到 7 个数,使这 7 个数之和等于 161? 若能,请由小到大依次写出这 7 个数;若不能,请说明理由.
(1)若将“H”形框上下左右移动,可框住 7 个数,若设“H”形框中的 7 个数中最中间一个数是 x,请用含 x 的代数式由小到大依次表示出“H”形框中的其余 6 个数;
(2)请问“H”形框能否框到 7 个数,使这 7 个数之和等于 161? 若能,请由小到大依次写出这 7 个数;若不能,请说明理由.

答案:解:(1)根据题意,得“H”形框中的其余 6 个数分别为$x-8,x-6,x-1,x+1,x+6,x+8$.
(2)能. 根据题意,得
$x-8+x-6+x-1+x+x+1+x+6+x+8=161$,
解得$x=23$,
故这 7 个数分别为 15,17,22,23,24,29,31.
(2)能. 根据题意,得
$x-8+x-6+x-1+x+x+1+x+6+x+8=161$,
解得$x=23$,
故这 7 个数分别为 15,17,22,23,24,29,31.
3. 某校给七年级(1)班全体学生准备了一定数量的练习本,若给每名学生发 3 本,则多 30 本,若给每名学生发 5 本,则少 50 本,请问该班有多少名学生?
答案:解:设该班有 x 名学生,
根据题意,得$3x+30=5x-50$,
解得$x=40$.
答:该班有 40 名学生.
根据题意,得$3x+30=5x-50$,
解得$x=40$.
答:该班有 40 名学生.
4. (2024·崇川区期末)某工厂需要生产一批太空漫步者(如图),每套设备由一个支架和两套脚踏板组装而成. 工厂现共有 45 名工人,每人每天平均生产 60 个支架或 96 套脚踏板.
(1)应如何分配工人才能使每天生产的支架和脚踏板恰好配套?
(2)若每套太空漫步者的成本为 240 元,要达到 20%的利润率,则每套应定价多少元?

(1)应如何分配工人才能使每天生产的支架和脚踏板恰好配套?
(2)若每套太空漫步者的成本为 240 元,要达到 20%的利润率,则每套应定价多少元?

答案:解:(1)设 x 人生产支架,则$(45-x)$人生产脚踏板,
根据题意,得$2×60x=96(45-x)$,
解得$x=20$,
则$45-x=45-20=25$.
答:20 人生产支架,25 人生产脚踏板.
(2)设每套应定价 a 元,
根据题意,得$a-240=240×20\% $,
解得$a=288$.
答:每套应定价 288 元.
根据题意,得$2×60x=96(45-x)$,
解得$x=20$,
则$45-x=45-20=25$.
答:20 人生产支架,25 人生产脚踏板.
(2)设每套应定价 a 元,
根据题意,得$a-240=240×20\% $,
解得$a=288$.
答:每套应定价 288 元.