1. 点动成
线
,线动成面
,面动成体
.答案:线 面 体
2. 图形之间常见的变换关系有
平移
、旋转
和翻折
.答案:平移 旋转 翻折
1. 下列生活现象中可以反映“面动成体”的是 (
A.流星划过夜空
B.打开折扇
C.汽车雨刷的转动
D.旋转门的旋转
D
)A.流星划过夜空
B.打开折扇
C.汽车雨刷的转动
D.旋转门的旋转
答案:D
2. 你见过一种折叠灯笼吗?如图,它看起来是平面的,可是提起来后却变成了美丽的灯笼,这个过程可近似地用哪个数学原理来解释 (
A.点动成线
B.线动成面
C.面动成体
D.面与面相交的地方是线
C
)A.点动成线
B.线动成面
C.面动成体
D.面与面相交的地方是线
答案:C
3. 把一枚硬币在桌面上竖直快速旋转后所形成的几何体是 (
A.圆柱
B.圆锥
C.球
D.正方体
C
)A.圆柱
B.圆锥
C.球
D.正方体
答案:C
解析:
把一枚硬币在桌面上竖直快速旋转后所形成的几何体是球。
答案:C
答案:C
4. 如图所示的平面图形绕直线l旋转一周,得到的立体图形是 (
D
)答案:D
5. 如图,仔细观察图案,并按规律在横线上画出合适的图案.


答案:
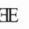
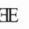
6. 如图,长方形的长和宽分别为6厘米和4厘米,分别绕它的长或宽所在直线旋转一周,得到不同的几何体,它们的体积分别为多少立方厘米?(结果保留π)


答案:解:绕长所在直线旋转一周得到的圆柱底面圆的半径为 4 厘米,高为 6 厘米,体积为 $\pi × 4^{2} × 6 = 96\pi$(立方厘米)。绕宽所在直线旋转一周得到的圆柱的底面圆的半径为 6 厘米,高为 4 厘米,体积为 $\pi × 6^{2} × 4 = 144\pi$(立方厘米)。