1. 如果两个角的度数之和等于
$90^{\circ}$
,那么这两个角互为余角,即其中一个角是另一个角的余角
.答案:$90^{\circ}$ 余角
2. 如果两个角的度数之和等于
$180^{\circ}$
,那么这两个角互为补角,即其中一个角是另一个角的补角
.答案:$180^{\circ}$ 补角
3. 同角(等角)的余角
随堂小练
相等
,同角(等角)的补角相等
.随堂小练
答案:相等 相等
1. (2024·吴江区二模)若$∠1 = 43^{\circ}$,则$∠1$的余角是 (
A.$43^{\circ}$
B.$47^{\circ}$
C.$57^{\circ}$
D.$137^{\circ}$
B
)A.$43^{\circ}$
B.$47^{\circ}$
C.$57^{\circ}$
D.$137^{\circ}$
答案:B
解析:
解:因为互为余角的两个角的和为$90^{\circ}$,所以$∠1$的余角为$90^{\circ} - ∠1$。
已知$∠1 = 43^{\circ}$,则$∠1$的余角为$90^{\circ} - 43^{\circ} = 47^{\circ}$。
答案:B
已知$∠1 = 43^{\circ}$,则$∠1$的余角为$90^{\circ} - 43^{\circ} = 47^{\circ}$。
答案:B
2. (2024·太仓月考)如图,点$O在直线AB$上,$∠COB = ∠EOD = 90^{\circ}$,下列说法错误的是 (
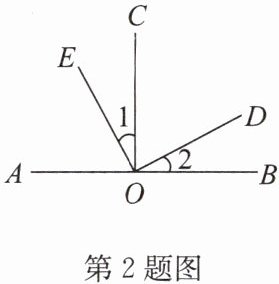
A.$∠1 = ∠2$
B.$∠AOE与∠2$互余
C.$∠AOD与∠1$互补
D.$∠AOD与∠COD$互补
D
)
A.$∠1 = ∠2$
B.$∠AOE与∠2$互余
C.$∠AOD与∠1$互补
D.$∠AOD与∠COD$互补
答案:D
解析:
∵点O在直线AB上,∠COB=∠EOD=90°
∴∠AOC=180°-∠COB=90°,∠1+∠COD=90°,∠2+∠COD=90°
∴∠1=∠2(A正确)
∵∠AOE+∠1=∠AOC=90°
∴∠AOE+∠2=90°,即∠AOE与∠2互余(B正确)
∵∠AOD=∠AOC+∠COD=90°+∠COD,∠1=90°-∠COD
∴∠AOD+∠1=90°+∠COD+90°-∠COD=180°,即∠AOD与∠1互补(C正确)
∵∠AOD=90°+∠COD
∴∠AOD+∠COD=90°+2∠COD,不一定等于180°(D错误)
答案:D
∴∠AOC=180°-∠COB=90°,∠1+∠COD=90°,∠2+∠COD=90°
∴∠1=∠2(A正确)
∵∠AOE+∠1=∠AOC=90°
∴∠AOE+∠2=90°,即∠AOE与∠2互余(B正确)
∵∠AOD=∠AOC+∠COD=90°+∠COD,∠1=90°-∠COD
∴∠AOD+∠1=90°+∠COD+90°-∠COD=180°,即∠AOD与∠1互补(C正确)
∵∠AOD=90°+∠COD
∴∠AOD+∠COD=90°+2∠COD,不一定等于180°(D错误)
答案:D
3. 若$∠α与∠β$互为补角,则下列式子成立的是 (
A.$∠α - ∠β = 180^{\circ}$
B.$∠α + ∠β = 90^{\circ}$
C.$∠α - ∠β = 90^{\circ}$
D.$∠α + ∠β = 180^{\circ}$
D
)A.$∠α - ∠β = 180^{\circ}$
B.$∠α + ∠β = 90^{\circ}$
C.$∠α - ∠β = 90^{\circ}$
D.$∠α + ∠β = 180^{\circ}$
答案:D
解析:
解:因为∠α与∠β互为补角,根据补角的定义,互为补角的两个角的和等于180°,所以∠α + ∠β = 180°。
D
D
4. 若$∠AOB + ∠BOC = 90^{\circ}$,$∠BOC与∠COD$互余,则$∠AOB与∠COD$的关系是 (
A.互余
B.互补
C.相等
D.不能确定
C
)A.互余
B.互补
C.相等
D.不能确定
答案:C
解析:
解:
∵∠AOB + ∠BOC = 90°,
∴∠AOB = 90° - ∠BOC。
∵∠BOC与∠COD互余,
∴∠BOC + ∠COD = 90°,
∴∠COD = 90° - ∠BOC。
∴∠AOB = ∠COD。
答案:C
∵∠AOB + ∠BOC = 90°,
∴∠AOB = 90° - ∠BOC。
∵∠BOC与∠COD互余,
∴∠BOC + ∠COD = 90°,
∴∠COD = 90° - ∠BOC。
∴∠AOB = ∠COD。
答案:C
5. $∠1$,$∠2都是∠3$的补角,根据
同角的补角相等
得$∠1 = ∠2$.答案:同角的补角相等
6. 如图,点$O在直线AB$上,$OD$,$OE分别平分∠BOC和∠AOC$,则图中互余的角共有

4
对.
答案:4
解析:
解:
∵点O在直线AB上,
∴∠AOB=180°,即∠AOC+∠BOC=180°.
∵OD平分∠BOC,OE平分∠AOC,
∴∠COE=∠AOE=1/2∠AOC,∠COD=∠BOD=1/2∠BOC.
∴∠COE+∠COD=1/2(∠AOC+∠BOC)=90°,即∠EOD=90°.
∴互余的角有:
∠COE与∠COD,∠COE与∠BOD,∠AOE与∠COD,∠AOE与∠BOD,共4对.
4
∵点O在直线AB上,
∴∠AOB=180°,即∠AOC+∠BOC=180°.
∵OD平分∠BOC,OE平分∠AOC,
∴∠COE=∠AOE=1/2∠AOC,∠COD=∠BOD=1/2∠BOC.
∴∠COE+∠COD=1/2(∠AOC+∠BOC)=90°,即∠EOD=90°.
∴互余的角有:
∠COE与∠COD,∠COE与∠BOD,∠AOE与∠COD,∠AOE与∠BOD,共4对.
4
7. 如图,点$O在直线AB$上,$∠AOD = ∠BOD = ∠EOC = 90^{\circ}$,$∠BOC:∠AOE = 3:1$.
(1)求$∠COD$的度数;
(2)图中有哪几对角互为补角?

(1)求$∠COD$的度数;
(2)图中有哪几对角互为补角?

答案:解:(1)因为$\angle AOD=\angle BOD=\angle EOC=90^{\circ}$,所以$\angle BOC+\angle AOE=90^{\circ}$。因为$\angle BOC:\angle AOE=3:1$,所以$\angle BOC=\frac{3}{4}×90^{\circ}=67.5^{\circ}$,所以$\angle COD=90^{\circ}-67.5^{\circ}=22.5^{\circ}$。(2)互补的角有:$\angle COB$与$\angle COA$,$\angle AOE$与$\angle EOB$,$\angle AOD$与$\angle BOD$,$\angle AOD$与$\angle EOC$,$\angle BOD$与$\angle EOC$,$\angle DOE$与$\angle COA$,$\angle COD$与$\angle EOB$。
解析:
(1)解:因为点$O$在直线$AB$上,$\angle AOD = \angle BOD = 90^{\circ}$,$\angle EOC = 90^{\circ}$,所以$\angle AOE + \angle EOD + \angle DOC + \angle COB = 180^{\circ}$,又因为$\angle EOD + \angle DOC = \angle EOC = 90^{\circ}$,所以$\angle AOE + \angle COB = 90^{\circ}$。
因为$\angle BOC:\angle AOE = 3:1$,设$\angle AOE = x$,则$\angle BOC = 3x$,可得$x + 3x = 90^{\circ}$,解得$x = 22.5^{\circ}$,所以$\angle BOC = 3x = 67.5^{\circ}$。
因为$\angle BOD = 90^{\circ}$,所以$\angle COD = \angle BOD - \angle BOC = 90^{\circ} - 67.5^{\circ} = 22.5^{\circ}$。
(2)互补的角有:$\angle COB$与$\angle COA$,$\angle AOE$与$\angle EOB$,$\angle AOD$与$\angle BOD$,$\angle AOD$与$\angle EOC$,$\angle BOD$与$\angle EOC$,$\angle DOE$与$\angle COA$,$\angle COD$与$\angle EOB$。
因为$\angle BOC:\angle AOE = 3:1$,设$\angle AOE = x$,则$\angle BOC = 3x$,可得$x + 3x = 90^{\circ}$,解得$x = 22.5^{\circ}$,所以$\angle BOC = 3x = 67.5^{\circ}$。
因为$\angle BOD = 90^{\circ}$,所以$\angle COD = \angle BOD - \angle BOC = 90^{\circ} - 67.5^{\circ} = 22.5^{\circ}$。
(2)互补的角有:$\angle COB$与$\angle COA$,$\angle AOE$与$\angle EOB$,$\angle AOD$与$\angle BOD$,$\angle AOD$与$\angle EOC$,$\angle BOD$与$\angle EOC$,$\angle DOE$与$\angle COA$,$\angle COD$与$\angle EOB$。
8. 一个角的补角加上$10^{\circ}后等于这个角的余角的3$倍,求这个角.
答案:解:设这个角为$x^{\circ}$,则它的余角为$90^{\circ}-x^{\circ}$,补角为$180^{\circ}-x^{\circ}$,根据题意,得$180^{\circ}-x^{\circ}+10^{\circ}=3×(90^{\circ}-x^{\circ})$,解得$x=40$。答:这个角为$40^{\circ}$。
解析:
解:设这个角为$x^{\circ}$,则它的余角为$(90 - x)^{\circ}$,补角为$(180 - x)^{\circ}$。
根据题意,得$180 - x + 10 = 3(90 - x)$
解方程:
$190 - x = 270 - 3x$
$-x + 3x = 270 - 190$
$2x = 80$
$x = 40$
答:这个角为$40^{\circ}$。
根据题意,得$180 - x + 10 = 3(90 - x)$
解方程:
$190 - x = 270 - 3x$
$-x + 3x = 270 - 190$
$2x = 80$
$x = 40$
答:这个角为$40^{\circ}$。