1. 两条直线相交所成的四个角中,有公共顶点没有公共边的两个角叫作
对顶角
。答案:对顶角
2. 对顶角的性质:两直线相交,对顶角
相等
。答案:相等
1. 下列四个选项的图形中,结论“$∠1= ∠2$”一定成立的是 (
C
)答案:C
2. 如图,直线AC和直线BD相交于点O,若$∠1+∠2= 90^{\circ }$,则$∠BOC$的度数是 (
A.$100^{\circ }$
B.$115^{\circ }$
C.$135^{\circ }$
D.$145^{\circ }$
C
)A.$100^{\circ }$
B.$115^{\circ }$
C.$135^{\circ }$
D.$145^{\circ }$
答案:C
解析:
解:∵直线AC和直线BD相交于点O,
∴∠1=∠2(对顶角相等)。
∵∠1+∠2=90°,
∴∠1=∠2=45°。
∵∠1+∠BOC=180°(邻补角互补),
∴∠BOC=180°-∠1=180°-45°=135°。
答案:C
∴∠1=∠2(对顶角相等)。
∵∠1+∠2=90°,
∴∠1=∠2=45°。
∵∠1+∠BOC=180°(邻补角互补),
∴∠BOC=180°-∠1=180°-45°=135°。
答案:C
3. 如图,直线AB,CD相交于点O,若$∠1= 26^{\circ }$,则$∠2= $
$26^{\circ}$
。答案:$26^{\circ}$
解析:
解:因为直线AB,CD相交于点O,所以∠1与∠2是对顶角。
根据对顶角相等,可得∠2=∠1=26°。
故∠2=26°。
根据对顶角相等,可得∠2=∠1=26°。
故∠2=26°。
4. 如图,直线AB与CD相交所成的四个角中,$∠1$的对顶角是
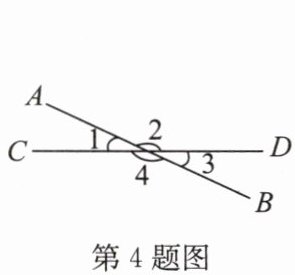
$∠3$
。
答案:$∠3$
5. (2024·如皋期末)如图,直线AB,CD相交于点O,若$∠BOC= 70^{\circ },∠DOE= 30^{\circ }$,则$∠AOE$的度数为
$40^{\circ}$
。答案:$40^{\circ}$
解析:
解:
∵直线AB,CD相交于点O,
∴∠AOD=∠BOC=70°(对顶角相等)。
∵∠DOE=30°,
∴∠AOE=∠AOD - ∠DOE=70° - 30°=40°。
40°
∵直线AB,CD相交于点O,
∴∠AOD=∠BOC=70°(对顶角相等)。
∵∠DOE=30°,
∴∠AOE=∠AOD - ∠DOE=70° - 30°=40°。
40°
6. 如图,直线AB,CD,EF相交于点O.
(1)写出$∠COE$的邻补角;
(2)分别写出$∠COE和∠BOE$的对顶角;
(3)如果$∠BOD= 60^{\circ },∠BOF= 90^{\circ }$,求$∠AOF和∠FOC$的度数。

(1)写出$∠COE$的邻补角;
(2)分别写出$∠COE和∠BOE$的对顶角;
(3)如果$∠BOD= 60^{\circ },∠BOF= 90^{\circ }$,求$∠AOF和∠FOC$的度数。

答案:(1)$∠COE$的邻补角为$∠COF$和$∠EOD$。(2)$∠COE$的对顶角为$∠DOF$,$∠BOE$的对顶角为$∠AOF$。(3)$∠AOF = 180^{\circ} - ∠BOF = 180^{\circ} - 90^{\circ} = 90^{\circ}$。因为$∠BOF = 90^{\circ}$,$∠BOD = 60^{\circ}$,所以$∠FOD = ∠BOF - ∠BOD = 90^{\circ} - 60^{\circ} = 30^{\circ}$,所以$∠FOC = 180^{\circ} - ∠FOD = 180^{\circ} - 30^{\circ} = 150^{\circ}$。
7. 如图,三条直线AB,CD,EF相交于点O,$∠1= 75^{\circ },∠2= 68^{\circ }$,求$∠COE$的度数。


答案:解:由角的和差,得$∠1 + ∠2 + ∠FOD = 180^{\circ}$,所以$∠FOD = 180^{\circ} - ∠1 - ∠2 = 180^{\circ} - 75^{\circ} - 68^{\circ} = 37^{\circ}$。由对顶角相等,得$∠COE = ∠FOD = 37^{\circ}$。