1. 如果两条直线相交所成的四个角中有一个角是
直角
,那么就称这两条直线互相垂直,它们的交点叫作垂足
。答案:直角 垂足
2. 在同一平面内,过一点有且只有
一
条直线与已知直线垂直。答案:一
1. (2024·鼓楼区期中)如图,过点 P 作线段 AB 的垂线,垂足在 (
A.线段 AB 上
B.线段 AB 的延长线上
C.线段 AB 的反向延长线上
D.直线 AB 外
B
)A.线段 AB 上
B.线段 AB 的延长线上
C.线段 AB 的反向延长线上
D.直线 AB 外
答案:B
解析:
根据垂线的定义,过点P作线段AB所在直线的垂线,观察图形可知,垂足位于点B的右侧,即线段AB的延长线上。
B
B
2. (2024·建邺区开学)$12:10$时针和分针所夹的较小角为 (
A.平角
B.钝角
C.直角
D.锐角
D
)A.平角
B.钝角
C.直角
D.锐角
答案:D
解析:
解:时针每分钟转0.5°,分针每分钟转6°。
12时10分,时针转过角度:10×0.5°=5°,分针转过角度:10×6°=60°。
夹角为:60°-5°=55°。
55°是锐角。
答案:D
12时10分,时针转过角度:10×0.5°=5°,分针转过角度:10×6°=60°。
夹角为:60°-5°=55°。
55°是锐角。
答案:D
3. 如图,直线 AB,CD 相交于点 O,若$∠EOD= 40^{\circ },∠BOC= 130^{\circ }$,那么射线 OE 与直线 AB 的位置关系是
OE ⊥ AB
。答案:OE ⊥ AB
解析:
解:
∵直线AB,CD相交于点O,
∴∠AOD=∠BOC=130°(对顶角相等)。
∵∠AOD=∠AOE+∠EOD,∠EOD=40°,
∴∠AOE=∠AOD-∠EOD=130°-40°=90°。
∴OE⊥AB。
答案:OE ⊥ AB
∵直线AB,CD相交于点O,
∴∠AOD=∠BOC=130°(对顶角相等)。
∵∠AOD=∠AOE+∠EOD,∠EOD=40°,
∴∠AOE=∠AOD-∠EOD=130°-40°=90°。
∴OE⊥AB。
答案:OE ⊥ AB
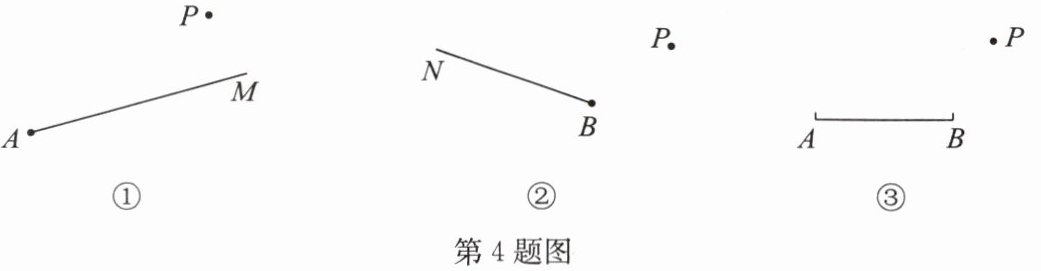
4. 如图,根据下列要求画图:
(1)如图①,过点 P 画射线 AM 的垂线,垂足为 Q;
(2)如图②,过点 P 画射线 BN 的垂线,交射线 BN 的反向延长线于点 Q;
(3)如图③,过点 P 画线段 AB 的垂线,交线段 AB 的延长线于点 Q。
(1)如图①,过点 P 画射线 AM 的垂线,垂足为 Q;
(2)如图②,过点 P 画射线 BN 的垂线,交射线 BN 的反向延长线于点 Q;
(3)如图③,过点 P 画线段 AB 的垂线,交线段 AB 的延长线于点 Q。

答案:
解:如答图.
解:如答图.

5. 如图,将两块三角尺的直角顶点 C 叠放在一起。
(1)若$∠DCE= 28^{\circ }$,求$∠ACB$的度数;
(2)若$∠ACB= 148^{\circ }$,求$∠DCE$的度数;
(3)直接写出$∠ACB与∠DCE$的数量关系。

(1)若$∠DCE= 28^{\circ }$,求$∠ACB$的度数;
(2)若$∠ACB= 148^{\circ }$,求$∠DCE$的度数;
(3)直接写出$∠ACB与∠DCE$的数量关系。

答案:解:(1)因为 $ \angle DCE = 28^{\circ} $, $ \angle ACD = \angle BCE = 90^{\circ} $,所以 $ \angle ACB = \angle ACD + \angle BCD = \angle ACD + \angle BCE - \angle DCE = 90^{\circ} + 90^{\circ} - 28^{\circ} = 152^{\circ} $.(2)因为 $ \angle ACB = 148^{\circ} $, $ \angle ECB = 90^{\circ} $,所以 $ \angle ACE = \angle ACB - \angle ECB = 148^{\circ} - 90^{\circ} = 58^{\circ} $.因为 $ \angle ACD = 90^{\circ} $,所以 $ \angle DCE = \angle ACD - \angle ACE = 90^{\circ} - 58^{\circ} = 32^{\circ} $.(3) $ \angle ACB + \angle DCE = 180^{\circ} $.
解析:
(1)解:因为∠DCE=28°,∠ACD=∠BCE=90°,所以∠ACB=∠ACD+∠BCE-∠DCE=90°+90°-28°=152°。
(2)解:因为∠ACB=148°,∠ECB=90°,所以∠ACE=∠ACB-∠ECB=148°-90°=58°。因为∠ACD=90°,所以∠DCE=∠ACD-∠ACE=90°-58°=32°。
(3)∠ACB+∠DCE=180°。
(2)解:因为∠ACB=148°,∠ECB=90°,所以∠ACE=∠ACB-∠ECB=148°-90°=58°。因为∠ACD=90°,所以∠DCE=∠ACD-∠ACE=90°-58°=32°。
(3)∠ACB+∠DCE=180°。