1. 在同一平面内,
不相交
的两条直线叫作平行线.答案:不相交
2. 过直线外一点
有且只有一
条直线与这条直线平行.答案:有且只有一
3. 在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线
平行
.答案:平行
1. 下列说法正确的是 (
A.同一平面内的两条直线叫平行线
B.两条平行线在同一平面内
C.不相交的两条直线叫平行线
D.过直线外一点有且只有一条直线与已知直线相交
B
)A.同一平面内的两条直线叫平行线
B.两条平行线在同一平面内
C.不相交的两条直线叫平行线
D.过直线外一点有且只有一条直线与已知直线相交
答案:B
解析:
解:A. 同一平面内不相交的两条直线叫平行线,故A错误;
B. 两条平行线在同一平面内,故B正确;
C. 同一平面内不相交的两条直线叫平行线,故C错误;
D. 过直线外一点有无数条直线与已知直线相交,故D错误。
结论:B
B. 两条平行线在同一平面内,故B正确;
C. 同一平面内不相交的两条直线叫平行线,故C错误;
D. 过直线外一点有无数条直线与已知直线相交,故D错误。
结论:B
2. (2024·江阴月考)在同一平面内两条不重合的直线的位置关系是 (
A.相交或垂直
B.平行或垂直
C.相交或平行
D.以上都不对
C
)A.相交或垂直
B.平行或垂直
C.相交或平行
D.以上都不对
答案:C
解析:
在同一平面内,两条不重合的直线,要么没有公共点,此时两直线平行;要么有且只有一个公共点,此时两直线相交。垂直是相交的一种特殊情况,并非独立的位置关系。所以位置关系是相交或平行。
C
C
3. 直线a与直线b互相平行,记作
$ a // b $
.答案:$ a // b $
解析:
$a// b$
4. 用三角尺和直尺画平行线.
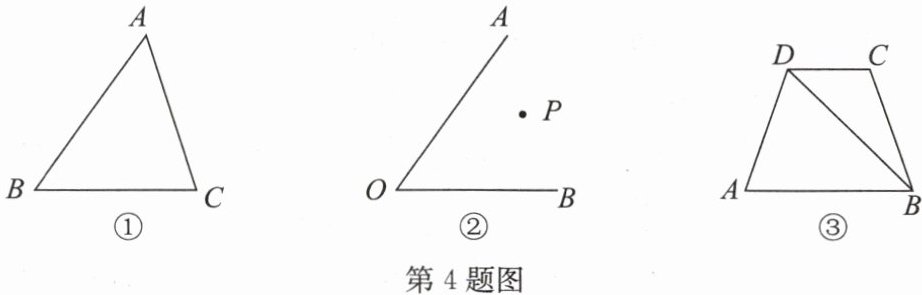
(1)如图①,过点A画MN//BC;
(2)如图②,过点P画PE//OA,交OB于点E,画PH//OB,交OA于点H;
(3)如图③,过点C画CE//DA,与AB交于点E,过点C画CF//DB,与AB的延长线交于点F.
(1)如图①,过点A画MN//BC;
(2)如图②,过点P画PE//OA,交OB于点E,画PH//OB,交OA于点H;
(3)如图③,过点C画CE//DA,与AB交于点E,过点C画CF//DB,与AB的延长线交于点F.

答案:
解:如答图所示.

解:如答图所示.

5. 如图,直线CD与直线AB相交于点C,过点P画PQ//CD,交AB于点Q.


答案:
解:如答图所示.

解:如答图所示.

6. 如图,在∠AOB内有一点P.
(1)过点P画$l_1//OA;$
(2)过点P画$l_2//OB;$
(3)用量角器量一量$l_1$与$l_2$相交所成的角与∠O有怎样的数量关系?

(1)过点P画$l_1//OA;$
(2)过点P画$l_2//OB;$
(3)用量角器量一量$l_1$与$l_2$相交所成的角与∠O有怎样的数量关系?

答案:
解:(1)(2)如答图所示.

(3)如答图,$ l_1 $与$ l_2 $相交所成的角有 4 个:$ \angle 1 $,$ \angle 2 $,$ \angle 3 $,$ \angle 4 $,其中$ \angle 1 = \angle 4 = \angle O $,$ \angle 2 + \angle O = \angle 3 + \angle O = 180^\circ $,所以$ l_1 $与$ l_2 $相交所成的角与$ \angle O $相等或互补.
解:(1)(2)如答图所示.

(3)如答图,$ l_1 $与$ l_2 $相交所成的角有 4 个:$ \angle 1 $,$ \angle 2 $,$ \angle 3 $,$ \angle 4 $,其中$ \angle 1 = \angle 4 = \angle O $,$ \angle 2 + \angle O = \angle 3 + \angle O = 180^\circ $,所以$ l_1 $与$ l_2 $相交所成的角与$ \angle O $相等或互补.