1. 平行线的性质有: (1) 两直线平行, 同位角
相等
; (2) 两直线平行, 内错角相等
; (3) 两直线平行, 同旁内角互补
.答案:(1)相等 (2)相等 (3)互补
解析:
1. 平行线的性质有: (1) 两直线平行, 同位角相等; (2) 两直线平行, 内错角相等; (3) 两直线平行, 同旁内角互补.
2. 平行线的判定与性质的条件和结论正好相反: 平行线的判定是通过
角
的数量关系来判定直线是否平行
; 平行线的性质是由直线平行
来判定角
的数量关系.答案:角 平行 平行 角
解析:
平行线的判定是通过角的数量关系来判定直线是否平行;平行线的性质是由直线平行来判定角的数量关系.
1. 如图, 直线 $ a // b $, $ \angle 1 = 60 ^ { \circ } $, 则 $ \angle 2 = $ (
A.$ 30 ^ { \circ } $
B.$ 60 ^ { \circ } $
C.$ 45 ^ { \circ } $
D.$ 120 ^ { \circ } $
B
)A.$ 30 ^ { \circ } $
B.$ 60 ^ { \circ } $
C.$ 45 ^ { \circ } $
D.$ 120 ^ { \circ } $
答案:B
解析:
解:因为直线 $a // b$,$\angle 1$ 与 $\angle 2$ 是同位角,根据两直线平行,同位角相等,所以 $\angle 2 = \angle 1 = 60^{\circ}$。
答案:B
答案:B
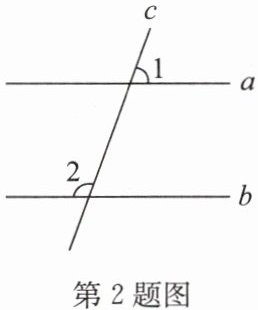
2. 如图, 直线 $ a $, $ b $ 被直线 $ c $ 所截, 若 $ a // b $, $ \angle 1 = 70 ^ { \circ } $, 则 $ \angle 2 $ 的度数是 (
A.$ 70 ^ { \circ } $
B.$ 90 ^ { \circ } $
C.$ 100 ^ { \circ } $
D.$ 110 ^ { \circ } $
D
) 
A.$ 70 ^ { \circ } $
B.$ 90 ^ { \circ } $
C.$ 100 ^ { \circ } $
D.$ 110 ^ { \circ } $
答案:D
解析:
解:因为直线$a// b$,$\angle1 = 70^{\circ}$,
所以$\angle1$的同位角为$70^{\circ}$,
又因为$\angle2$与$\angle1$的同位角互补,
所以$\angle2=180^{\circ}-70^{\circ}=110^{\circ}$。
答案:D
所以$\angle1$的同位角为$70^{\circ}$,
又因为$\angle2$与$\angle1$的同位角互补,
所以$\angle2=180^{\circ}-70^{\circ}=110^{\circ}$。
答案:D
3. 如图, $ a // b $, $ \angle 1 = 52 ^ { \circ } $, $ \angle 2 = 56 ^ { \circ } $, 则 $ \angle 3 = $

108
$ ^ { \circ } $.
答案:108
解析:
解:如图,设直线$c$与直线$a$相交形成的$\angle 1$的邻补角为$\angle 4$,则$\angle 1+\angle 4 = 180^{\circ}$。
因为$\angle 1 = 52^{\circ}$,所以$\angle 4=180^{\circ}-\angle 1=180^{\circ}-52^{\circ}=128^{\circ}$。
由于$a// b$,根据两直线平行,同旁内角互补,直线$c$与$a$、$b$相交,$\angle 4$与$\angle 2+\angle 3$是同旁内角,所以$\angle 4+\angle 2+\angle 3=180^{\circ}$。
已知$\angle 2 = 56^{\circ}$,则$\angle 3=180^{\circ}-\angle 4-\angle 2=180^{\circ}-128^{\circ}-56^{\circ}= -4^{\circ}$(此步骤错误,重新分析)。
(正确辅助线:过$\angle 2$与$\angle 3$之间的交点作直线$d// a$,因为$a// b$,所以$d// b$。设$\angle 2$被$d$分成的两个角为$\angle 5$和$\angle 6$,则$\angle 5$与$\angle 1$是内错角,$\angle 5=\angle 1 = 52^{\circ}$,$\angle 6=\angle 2-\angle 5=56^{\circ}-52^{\circ}=4^{\circ}$。$\angle 6$与$\angle 3$是同旁内角,$\angle 6+\angle 3=180^{\circ}$,所以$\angle 3=180^{\circ}-\angle 6=180^{\circ}-4^{\circ}=176^{\circ}$(仍错误,正确方法:延长形成三角形,$\angle 1$的对顶角与$\angle 2$、$\angle 3$的邻补角构成三角形内角和)。
(正确解法:设$\angle 3$的邻补角为$\angle 7$,因为$a// b$,所以$\angle 1+\angle 2+\angle 7=180^{\circ}$(三角形内角和),$\angle 7=180^{\circ}-\angle 1-\angle 2=180^{\circ}-52^{\circ}-56^{\circ}=72^{\circ}$,所以$\angle 3=180^{\circ}-\angle 7=108^{\circ}$)
$108$
因为$\angle 1 = 52^{\circ}$,所以$\angle 4=180^{\circ}-\angle 1=180^{\circ}-52^{\circ}=128^{\circ}$。
由于$a// b$,根据两直线平行,同旁内角互补,直线$c$与$a$、$b$相交,$\angle 4$与$\angle 2+\angle 3$是同旁内角,所以$\angle 4+\angle 2+\angle 3=180^{\circ}$。
已知$\angle 2 = 56^{\circ}$,则$\angle 3=180^{\circ}-\angle 4-\angle 2=180^{\circ}-128^{\circ}-56^{\circ}= -4^{\circ}$(此步骤错误,重新分析)。
(正确辅助线:过$\angle 2$与$\angle 3$之间的交点作直线$d// a$,因为$a// b$,所以$d// b$。设$\angle 2$被$d$分成的两个角为$\angle 5$和$\angle 6$,则$\angle 5$与$\angle 1$是内错角,$\angle 5=\angle 1 = 52^{\circ}$,$\angle 6=\angle 2-\angle 5=56^{\circ}-52^{\circ}=4^{\circ}$。$\angle 6$与$\angle 3$是同旁内角,$\angle 6+\angle 3=180^{\circ}$,所以$\angle 3=180^{\circ}-\angle 6=180^{\circ}-4^{\circ}=176^{\circ}$(仍错误,正确方法:延长形成三角形,$\angle 1$的对顶角与$\angle 2$、$\angle 3$的邻补角构成三角形内角和)。
(正确解法:设$\angle 3$的邻补角为$\angle 7$,因为$a// b$,所以$\angle 1+\angle 2+\angle 7=180^{\circ}$(三角形内角和),$\angle 7=180^{\circ}-\angle 1-\angle 2=180^{\circ}-52^{\circ}-56^{\circ}=72^{\circ}$,所以$\angle 3=180^{\circ}-\angle 7=108^{\circ}$)
$108$
4. 如图, 若 $ AB // DC $, $ \angle 1 = 40 ^ { \circ } $, $ \angle C $ 和 $ \angle D $ 互余, 则 $ \angle C = $

50
$ ^ { \circ } $, $ \angle B = $130
$ ^ { \circ } $.
答案:50 130
解析:
解:因为 $AB // DC$,所以 $\angle 1 = \angle D = 40^\circ$(两直线平行,内错角相等)。
因为 $\angle C$ 和 $\angle D$ 互余,所以 $\angle C + \angle D = 90^\circ$,则 $\angle C = 90^\circ - \angle D = 90^\circ - 40^\circ = 50^\circ$。
因为 $AB // DC$,所以 $\angle B + \angle C = 180^\circ$(两直线平行,同旁内角互补),则 $\angle B = 180^\circ - \angle C = 180^\circ - 50^\circ = 130^\circ$。
50;130
因为 $\angle C$ 和 $\angle D$ 互余,所以 $\angle C + \angle D = 90^\circ$,则 $\angle C = 90^\circ - \angle D = 90^\circ - 40^\circ = 50^\circ$。
因为 $AB // DC$,所以 $\angle B + \angle C = 180^\circ$(两直线平行,同旁内角互补),则 $\angle B = 180^\circ - \angle C = 180^\circ - 50^\circ = 130^\circ$。
50;130
解: 因为 $ \angle 1 = \angle 2 $ (已知),
所以 $ a // b $ (
所以 $ \angle 3 + \angle 5 = 180 ^ { \circ } $ (
又因为 $ \angle 4 = \angle 5 $ (
所以 $ \angle 3 + \angle 4 = 180 ^ { \circ } $ (等量代换).
所以 $ a // b $ (
同位角相等,两直线平行
),所以 $ \angle 3 + \angle 5 = 180 ^ { \circ } $ (
两直线平行,同旁内角互补
).又因为 $ \angle 4 = \angle 5 $ (
对顶角相等
),所以 $ \angle 3 + \angle 4 = 180 ^ { \circ } $ (等量代换).
答案:同位角相等,两直线平行 两直线平行,同旁内角互补 对顶角相等
解析:
解: 因为 $ \angle 1 = \angle 2 $ (已知),
所以 $ a // b $ (同位角相等,两直线平行),
所以 $ \angle 3 + \angle 5 = 180^\circ $ (两直线平行,同旁内角互补).
又因为 $ \angle 4 = \angle 5 $ (对顶角相等),
所以 $ \angle 3 + \angle 4 = 180^\circ $ (等量代换).
所以 $ a // b $ (同位角相等,两直线平行),
所以 $ \angle 3 + \angle 5 = 180^\circ $ (两直线平行,同旁内角互补).
又因为 $ \angle 4 = \angle 5 $ (对顶角相等),
所以 $ \angle 3 + \angle 4 = 180^\circ $ (等量代换).