1. 填空题。
(1) 一个正方体, 棱长是 8 分米, 它的棱长总和是(
(2) 一个长方体纸盒, 长 60 厘米, 宽 40 厘米, 高 30 厘米,这个纸盒的体积是(
(1) 一个正方体, 棱长是 8 分米, 它的棱长总和是(
96
)分米, 表面积是(384
)平方分米, 体积是(512
)立方分米。(2) 一个长方体纸盒, 长 60 厘米, 宽 40 厘米, 高 30 厘米,这个纸盒的体积是(
72000
)立方厘米。如果把这个纸盒展开放在桌面上, 所占桌面的面积是(10800
)平方厘米。答案:(1)96,384,512;(2)72000,10800
解析:
(1)正方体棱长总和=棱长×12,8×12=96(分米);表面积=棱长×棱长×6,8×8×6=384(平方分米);体积=棱长×棱长×棱长,8×8×8=512(立方分米)。
(2)长方体体积=长×宽×高,60×40×30=72000(立方厘米);展开后所占桌面面积即表面积,(60×40+60×30+40×30)×2=(2400+1800+1200)×2=5400×2=10800(平方厘米)。
(2)长方体体积=长×宽×高,60×40×30=72000(立方厘米);展开后所占桌面面积即表面积,(60×40+60×30+40×30)×2=(2400+1800+1200)×2=5400×2=10800(平方厘米)。
2. 填表。
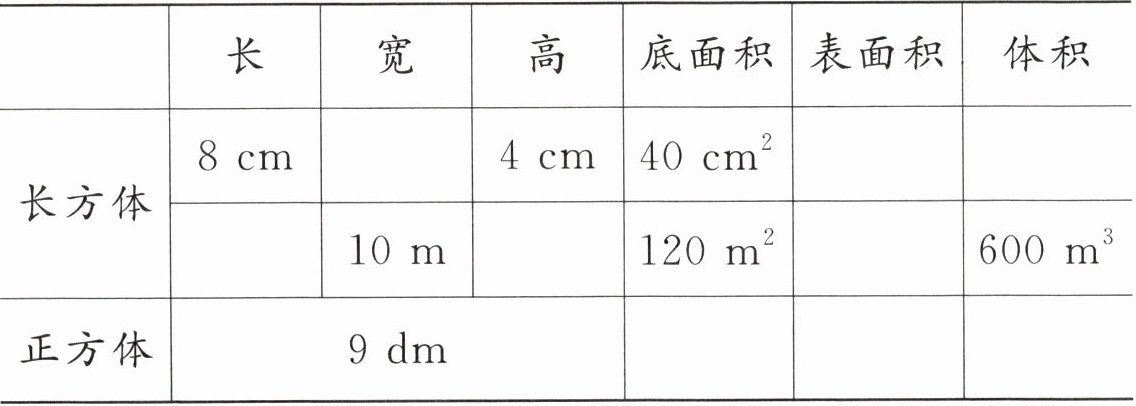
| | 长 | 宽 | 高 | 底面积 | 表面积 | 体积 |
| --- | --- | --- | --- | --- | --- | --- |
| 长方体 | 8 cm | 5 cm | 4 cm | $40 cm^{2}$ | $184 cm^{2}$ | $160 cm^{3}$ |
| | 12 m | 10 m | 5 m | $120 m^{2}$ | $460 m^{2}$ | $600 m^{3}$ |
| 正方体 | 9 dm | 9 dm | 9 dm | $81 dm^{2}$ | $486 dm^{2}$ | $729 dm^{3}$ |

| | 长 | 宽 | 高 | 底面积 | 表面积 | 体积 |
| --- | --- | --- | --- | --- | --- | --- |
| 长方体 | 8 cm | 5 cm | 4 cm | $40 cm^{2}$ | $184 cm^{2}$ | $160 cm^{3}$ |
| | 12 m | 10 m | 5 m | $120 m^{2}$ | $460 m^{2}$ | $600 m^{3}$ |
| 正方体 | 9 dm | 9 dm | 9 dm | $81 dm^{2}$ | $486 dm^{2}$ | $729 dm^{3}$ |
答案:1. 对于第一个长方体:
宽:根据底面积公式$S = a× b$($S$为底面积,$a$为长,$b$为宽),已知$a = 8cm$,$S=40cm^{2}$,则宽$b=S÷ a = 40÷8 = 5cm$。
表面积:$S_{表}=(ab + ah+bh)×2=(8×5 + 8×4+5×4)×2=(40 + 32 + 20)×2=92×2 = 184cm^{2}$。
体积:$V = a× b× h=8×5×4 = 160cm^{3}$。
2. 对于第二个长方体:
长:根据底面积公式$S = a× b$,已知$b = 10m$,$S = 120m^{2}$,则长$a=S÷ b=120÷10 = 12m$。
高:根据体积公式$V=a× b× h$,已知$V = 600m^{3}$,$a = 12m$,$b = 10m$,则高$h=V÷(a× b)=600÷120 = 5m$。
表面积:$S_{表}=(ab + ah+bh)×2=(12×10+12×5 + 10×5)×2=(120+60 + 50)×2=230×2 = 460m^{2}$。
3. 对于正方体:
宽和高:因为正方体的$12$条棱都相等,所以宽$=$高$ = 9dm$。
底面积:$S=a× a=9×9 = 81dm^{2}$。
表面积:$S_{表}=6× a× a=6×81 = 486dm^{2}$。
体积:$V=a× a× a=9×9×9 = 729dm^{3}$。
填表如下:
| | 长 | 宽 | 高 | 底面积 | 表面积 | 体积 |
| --- | --- | --- | --- | --- | --- | --- |
| 长方体 | 8 cm | 5 cm | 4 cm | $40 cm^{2}$ | $184 cm^{2}$ | $160 cm^{3}$ |
| | 12 m | 10 m | 5 m | $120 m^{2}$ | $460 m^{2}$ | $600 m^{3}$ |
| 正方体 | 9 dm | 9 dm | 9 dm | $81 dm^{2}$ | $486 dm^{2}$ | $729 dm^{3}$ |
宽:根据底面积公式$S = a× b$($S$为底面积,$a$为长,$b$为宽),已知$a = 8cm$,$S=40cm^{2}$,则宽$b=S÷ a = 40÷8 = 5cm$。
表面积:$S_{表}=(ab + ah+bh)×2=(8×5 + 8×4+5×4)×2=(40 + 32 + 20)×2=92×2 = 184cm^{2}$。
体积:$V = a× b× h=8×5×4 = 160cm^{3}$。
2. 对于第二个长方体:
长:根据底面积公式$S = a× b$,已知$b = 10m$,$S = 120m^{2}$,则长$a=S÷ b=120÷10 = 12m$。
高:根据体积公式$V=a× b× h$,已知$V = 600m^{3}$,$a = 12m$,$b = 10m$,则高$h=V÷(a× b)=600÷120 = 5m$。
表面积:$S_{表}=(ab + ah+bh)×2=(12×10+12×5 + 10×5)×2=(120+60 + 50)×2=230×2 = 460m^{2}$。
3. 对于正方体:
宽和高:因为正方体的$12$条棱都相等,所以宽$=$高$ = 9dm$。
底面积:$S=a× a=9×9 = 81dm^{2}$。
表面积:$S_{表}=6× a× a=6×81 = 486dm^{2}$。
体积:$V=a× a× a=9×9×9 = 729dm^{3}$。
填表如下:
| | 长 | 宽 | 高 | 底面积 | 表面积 | 体积 |
| --- | --- | --- | --- | --- | --- | --- |
| 长方体 | 8 cm | 5 cm | 4 cm | $40 cm^{2}$ | $184 cm^{2}$ | $160 cm^{3}$ |
| | 12 m | 10 m | 5 m | $120 m^{2}$ | $460 m^{2}$ | $600 m^{3}$ |
| 正方体 | 9 dm | 9 dm | 9 dm | $81 dm^{2}$ | $486 dm^{2}$ | $729 dm^{3}$ |
1. 从一块长 18 厘米、宽 15 厘米、高 10 厘米的长方体木料上锯下一个最大的正方体, 锯下的这个正方体的体积是多少? 剩余部分的体积是多少?
答案:1 1000 立方厘米 1700 立方厘米
解析:
正方体的棱长为长方体长、宽、高中的最小值,即10厘米。
正方体体积:$10×10×10 = 1000$(立方厘米)
长方体体积:$18×15×10 = 2700$(立方厘米)
剩余部分体积:$2700 - 1000 = 1700$(立方厘米)
锯下的正方体体积是1000立方厘米,剩余部分体积是1700立方厘米。
正方体体积:$10×10×10 = 1000$(立方厘米)
长方体体积:$18×15×10 = 2700$(立方厘米)
剩余部分体积:$2700 - 1000 = 1700$(立方厘米)
锯下的正方体体积是1000立方厘米,剩余部分体积是1700立方厘米。
2. 小明先用铁丝制作了一个长 3 分米、宽 2.5 分米、高 4 分米的长方体框架, 再在各个面贴上红纸, 做成了一个捐款箱。制作这样一个捐款箱, 至少需要铁丝多少米? 需要红纸多少平方分米? (开口和接口均忽略不计)


答案:2 3.8 米 59 平方分米
解析:
长方体棱长总和=(长+宽+高)×4=(3+2.5+4)×4=9.5×4=38(分米)=3.8米
长方体表面积=(长×宽+长×高+宽×高)×2=(3×2.5+3×4+2.5×4)×2=(7.5+12+10)×2=29.5×2=59(平方分米)
至少需要铁丝3.8米,需要红纸59平方分米。
长方体表面积=(长×宽+长×高+宽×高)×2=(3×2.5+3×4+2.5×4)×2=(7.5+12+10)×2=29.5×2=59(平方分米)
至少需要铁丝3.8米,需要红纸59平方分米。
3. 工人师傅将一块棱长 15 厘米的正方体钢锭熔铸成一根横截面是正方形的钢条。已知这根钢条的横截面边长是 3 厘米, 算一算, 加工成的钢条长多少米?
答案:3 3.75 米
解析:
正方体钢锭体积:$15×15×15 = 3375$(立方厘米)
钢条横截面积:$3×3 = 9$(平方厘米)
钢条长度:$3375÷9 = 375$(厘米)
$375$厘米$= 3.75$米
答:加工成的钢条长$3.75$米。
钢条横截面积:$3×3 = 9$(平方厘米)
钢条长度:$3375÷9 = 375$(厘米)
$375$厘米$= 3.75$米
答:加工成的钢条长$3.75$米。