1 右图表示某早餐店做包子所需三种原料的份数。
(1) 做包子所用的面粉、鲜肉、青菜的质量比是(
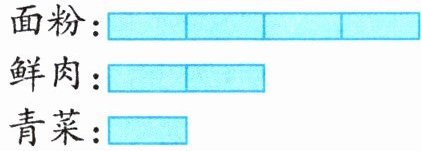
(2) 早餐店做包子使用这三种原料共 112 千克,三种原料各使用多少千克?
(3) 如果三种原料都有 24 千克,要将鲜肉全部用完,那么要添加多少千克面粉?还剩多少千克青菜?
(1) 做包子所用的面粉、鲜肉、青菜的质量比是(
4:2:1
)。
(2) 早餐店做包子使用这三种原料共 112 千克,三种原料各使用多少千克?
面粉:64 千克 鲜肉:32 千克 青菜:16 千克
(3) 如果三种原料都有 24 千克,要将鲜肉全部用完,那么要添加多少千克面粉?还剩多少千克青菜?
24 千克 12 千克
答案:1
(1)4:2:1
(2)面粉:64 千克 鲜肉:32 千克 青菜:16 千克
(3)24 千克 12 千克
(1)4:2:1
(2)面粉:64 千克 鲜肉:32 千克 青菜:16 千克
(3)24 千克 12 千克
2 用 35 厘米长的铁丝围成一个等腰三角形。已知一条腰与底的长度比是 $3:1$,则它的一条腰长(
15
)厘米。答案:15
解析:
3+3+1=7
35×$\frac{3}{7}$=15
15
35×$\frac{3}{7}$=15
15
3 某水果店运进梨和苹果的质量比是 $3:2$,当卖出 15 千克梨后,苹果的质量与梨的质量相等。梨和苹果原来各有多少千克?
答案:梨:45 千克 苹果:30 千克
解析:
设梨原来有$3x$千克,苹果原来有$2x$千克。
$3x - 15 = 2x$
$3x - 2x = 15$
$x = 15$
梨:$3x = 3×15 = 45$(千克)
苹果:$2x = 2×15 = 30$(千克)
答:梨原来有45千克,苹果原来有30千克。
$3x - 15 = 2x$
$3x - 2x = 15$
$x = 15$
梨:$3x = 3×15 = 45$(千克)
苹果:$2x = 2×15 = 30$(千克)
答:梨原来有45千克,苹果原来有30千克。
4 在下面的方格纸上画一个平行四边形,面积是 36 平方厘米,底和高的比是 $4:1$。(假设方格纸上每个小方格的边长为 1 厘米)


答案:设高为$x$厘米,因为底和高的比是$4:1$,所以底为$4x$厘米。
根据平行四边形面积公式$S = 底×高$,可得$4x\cdot x = 36$,即$4x^{2}=36$,$x^{2}=9$,解得$x = 3$($x=-3$舍去)。
所以高为$3$厘米,底为$4×3 = 12$厘米。
在方格纸中画底为$12$格(横向),高为$3$格(竖向距离底边)的平行四边形(画法不唯一)。
根据平行四边形面积公式$S = 底×高$,可得$4x\cdot x = 36$,即$4x^{2}=36$,$x^{2}=9$,解得$x = 3$($x=-3$舍去)。
所以高为$3$厘米,底为$4×3 = 12$厘米。
在方格纸中画底为$12$格(横向),高为$3$格(竖向距离底边)的平行四边形(画法不唯一)。
5 右边平行四边形的面积是 20 平方厘米,图中甲、乙、丙 3 个三角形的面积比是(

5:2:3
),涂色部分的面积是(6
)平方厘米。
答案:5:2:3 6
解析:
设平行四边形的高为$h$厘米,底边长为$2 + 3=5$厘米。
因为平行四边形面积为$20$平方厘米,所以$5h = 20$,解得$h = 4$。
甲三角形底为$5$厘米,高为$h = 4$厘米,面积$S_{甲}=\frac{1}{2}×5×4 = 10$平方厘米。
乙三角形底为$2$厘米,高为$h = 4$厘米,面积$S_{乙}=\frac{1}{2}×2×4 = 4$平方厘米。
丙三角形底为$3$厘米,高为$h = 4$厘米,面积$S_{丙}=\frac{1}{2}×3×4 = 6$平方厘米。
甲、乙、丙面积比为$10:4:6 = 5:2:3$,涂色部分为丙,面积是$6$平方厘米。
5:2:3 6
因为平行四边形面积为$20$平方厘米,所以$5h = 20$,解得$h = 4$。
甲三角形底为$5$厘米,高为$h = 4$厘米,面积$S_{甲}=\frac{1}{2}×5×4 = 10$平方厘米。
乙三角形底为$2$厘米,高为$h = 4$厘米,面积$S_{乙}=\frac{1}{2}×2×4 = 4$平方厘米。
丙三角形底为$3$厘米,高为$h = 4$厘米,面积$S_{丙}=\frac{1}{2}×3×4 = 6$平方厘米。
甲、乙、丙面积比为$10:4:6 = 5:2:3$,涂色部分为丙,面积是$6$平方厘米。
5:2:3 6
1 如果甲数与乙数的比是 $4:5$,乙数与丙数的比是 $3:4$,那甲数:丙数 $=$ (
3
):(5
)。答案:3:5
解析:
甲数与乙数的比是$4:5$,乙数与丙数的比是$3:4$。
将乙数的份数统一,$5$和$3$的最小公倍数是$15$。
甲数:乙数$=4:5=(4×3):(5×3)=12:15$
乙数:丙数$=3:4=(3×5):(4×5)=15:20$
所以甲数:丙数$=12:20=3:5$
$3$;$5$
将乙数的份数统一,$5$和$3$的最小公倍数是$15$。
甲数:乙数$=4:5=(4×3):(5×3)=12:15$
乙数:丙数$=3:4=(3×5):(4×5)=15:20$
所以甲数:丙数$=12:20=3:5$
$3$;$5$
2 今年爸爸与儿子的年龄比是 $7:1$,爸爸今年 28 岁,多少年后,父子两人的年龄比是 $19:7$?
答案:10 年
解析:
儿子今年年龄:$28÷7 = 4$(岁)
设$x$年后父子年龄比是$19:7$,则$\frac{28 + x}{4 + x}=\frac{19}{7}$
$7(28 + x)=19(4 + x)$
$196 + 7x=76 + 19x$
$12x=120$
$x = 10$
10年
设$x$年后父子年龄比是$19:7$,则$\frac{28 + x}{4 + x}=\frac{19}{7}$
$7(28 + x)=19(4 + x)$
$196 + 7x=76 + 19x$
$12x=120$
$x = 10$
10年