(1)$30÷$(
50
)$= \frac{3}{5}= 6:$(10
)$=$(60
)$\%=$(六
)折$=$(0.6
)(小数)答案:(1)50,10, 60,六,0.6。
解析:
$30 ÷ (\space )$ = $\frac{3}{5}$,可以转化为$30 ÷ (\space )$ = $0.6$,所以( )=$50$。
$\frac{3}{5} = 3:5$,同时乘以2,得到$6:10$,所以( )=$10$。
$\frac{3}{5} = 0.6$,转化为百分数,即$60\%$,所以( )=$60$。
$60\%$转化为折扣,即六折,所以( )=$六$。
$\frac{3}{5}$转化为小数,即$0.6$,所以( )=$0.6$。
$\frac{3}{5} = 3:5$,同时乘以2,得到$6:10$,所以( )=$10$。
$\frac{3}{5} = 0.6$,转化为百分数,即$60\%$,所以( )=$60$。
$60\%$转化为折扣,即六折,所以( )=$六$。
$\frac{3}{5}$转化为小数,即$0.6$,所以( )=$0.6$。
(2)一种商品降价$12\%$,现价是原价的(
88
)$\%$。答案:$88$
解析:
把原价看作单位“1”,商品降价$12\%$,则现价是原价的$1 - 12\%=100\% - 12\% = 88\%$。
(3)某市 2021 年的国内生产总值是前一年的$125\%$,该市 2021 年国内生产总值比 2020 年增加(
25
)%。答案:25
解析:
把2020年国内生产总值看作单位“1”,2021年是2020年的125%,增加的百分比为125% - 1 = 25%。
(4)某食堂三月份烧煤 5 吨,计划用煤 8 吨。实际用煤比计划节约(
37.5
)%,计划用煤比实际多(60
)%。答案:$37.5$,$60$
解析:
1. 计算实际用煤比计划节约的百分比:
实际比计划节约的数量为:$8 - 5=3$(吨)。
节约的百分比为:$\frac{8 - 5}{8}×100\%=\frac{3}{8}×100\% = 37.5\%$。
2. 计算计划用煤比实际多的百分比:
计划比实际多的数量也是3吨。
多的百分比为:$\frac{8 - 5}{5}×100\%=\frac{3}{5}×100\%=60\%$。
实际比计划节约的数量为:$8 - 5=3$(吨)。
节约的百分比为:$\frac{8 - 5}{8}×100\%=\frac{3}{8}×100\% = 37.5\%$。
2. 计算计划用煤比实际多的百分比:
计划比实际多的数量也是3吨。
多的百分比为:$\frac{8 - 5}{5}×100\%=\frac{3}{5}×100\%=60\%$。
(5)将$0.85$、$0.\dot{8}\dot{5}$、$\frac{6}{7}$、$85.5\%$按从小到大的顺序排列起来:(
$0.85$
)<($85.5\%$
)<($\frac{6}{7}$
)<($0.\dot{8}\dot{5}$
)。答案:$0.85<85.5\%<\frac{6}{7}<0.\dot{8}\dot{5}$(对应顺序填空即可,此处理解为填原始形式顺序)
解析:
将各数转化为小数进行比较:
$0.85$ 保持不变。
$0.\dot{8}\dot{5}=0.858585...$
$\frac{6}{7}\approx0.857143$
$85.5\%=0.855$
比较得:$0.85<0.855<0.857143<0.858585...$。
所以从小到大的顺序为:$0.85<85.5\%<\frac{6}{7}<0.\dot{8}\dot{5}$。
$0.85$ 保持不变。
$0.\dot{8}\dot{5}=0.858585...$
$\frac{6}{7}\approx0.857143$
$85.5\%=0.855$
比较得:$0.85<0.855<0.857143<0.858585...$。
所以从小到大的顺序为:$0.85<85.5\%<\frac{6}{7}<0.\dot{8}\dot{5}$。
(6)右图中,涂色部分的面积占大正方形面积的(
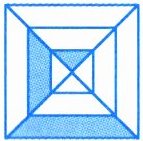
25
)%。
答案:【解析】:设大正方形边长为2,则面积为2×2=4。假设涂色部分为边长1的小正方形,面积为1×1=1。1÷4=0.25=25%。
【答案】:25
【答案】:25
(7)一辆自行车,原价是 240 元,现在打八折出售,现价比原价少(
48
)元。答案:48
解析:
原价为240元,打八折即现价为原价的80%。
计算现价:$240 × 0.8 = 192$(元)。
现价比原价少:$240 - 192 = 48$(元)。
计算现价:$240 × 0.8 = 192$(元)。
现价比原价少:$240 - 192 = 48$(元)。
(8)一个榨油厂用 340 千克芝麻榨出 153 千克油,芝麻的出油率是(
45
)%。答案:$45$
解析:
出油率的计算公式为:$出油率 = \left( \frac{榨出的油的重量}{芝麻的总重量} \right) × 100\%$。
将题目中的数据代入公式:
$出油率 = \left( \frac{153}{340} \right) × 100\% = 45\%$。
将题目中的数据代入公式:
$出油率 = \left( \frac{153}{340} \right) × 100\% = 45\%$。
(9)最小的合数比最小的质数多(
100
)%。答案:100
解析:
最小的合数是4,最小的质数是2。先求4比2多的数:4-2=2,再求多的数占最小质数的百分比:2÷2×100%=100%。
2 判断题。(对的画“√”,错的画“×”)(每题 3 分,共 12 分)
(1)一根绳子长$\frac{3}{4}$米,也就是$75\%$米。 (
(2)10 千克先减少$10\%$,再增加$10\%$,结果还是 10 千克。 (
(3)松树的棵数比柏树的多$30\%$,柏树的棵数就比松树的少$30\%$。 (
(4)在含盐$10\%$的盐水中,盐与水的比是$1:9$。 (
(1)一根绳子长$\frac{3}{4}$米,也就是$75\%$米。 (
×
)(2)10 千克先减少$10\%$,再增加$10\%$,结果还是 10 千克。 (
×
)(3)松树的棵数比柏树的多$30\%$,柏树的棵数就比松树的少$30\%$。 (
×
)(4)在含盐$10\%$的盐水中,盐与水的比是$1:9$。 (
√
)答案:(1)× (2)× (3)× (4)√
解析:
(1)百分数表示一个数是另一个数的百分之几,它表示的是两个数的比例关系,后面不能带单位名称。
$\frac{3}{4}$米是具体的长度,而$75\%$不能表示具体的长度,所以该说法错误,应画“×”。
(2)先把10千克看成单位“$1$”,减少$10\%$后的重量是$10×(1 - 10\%)=10×0.9 = 9$千克;再把9千克看成单位“$1$”,增加$10\%$后的重量是$9×(1 + 10\%)=9×1.1 = 9.9$千克,$9.9\neq10$,所以该说法错误,应画“×”。
(3)设柏树的棵数是$100$棵,松树的棵数比柏树的多$30\%$,则松树的棵数是$100×(1 + 30\%)=130$棵。此时柏树比松树少$(130 - 100)÷130\approx23.1\%$,不是$30\%$,所以该说法错误,应画“×”。
(4)含盐$10\%$的盐水,把盐水看成单位“$1$”,盐占$10\%$,那么水占$1 - 10\% = 90\%$,所以盐与水的比是$10\%:90\% = 1:9$,该说法正确,应画“√”。
$\frac{3}{4}$米是具体的长度,而$75\%$不能表示具体的长度,所以该说法错误,应画“×”。
(2)先把10千克看成单位“$1$”,减少$10\%$后的重量是$10×(1 - 10\%)=10×0.9 = 9$千克;再把9千克看成单位“$1$”,增加$10\%$后的重量是$9×(1 + 10\%)=9×1.1 = 9.9$千克,$9.9\neq10$,所以该说法错误,应画“×”。
(3)设柏树的棵数是$100$棵,松树的棵数比柏树的多$30\%$,则松树的棵数是$100×(1 + 30\%)=130$棵。此时柏树比松树少$(130 - 100)÷130\approx23.1\%$,不是$30\%$,所以该说法错误,应画“×”。
(4)含盐$10\%$的盐水,把盐水看成单位“$1$”,盐占$10\%$,那么水占$1 - 10\% = 90\%$,所以盐与水的比是$10\%:90\% = 1:9$,该说法正确,应画“√”。
(1)一台电视机原价 4800 元,现在每台只卖 3840 元,相当于降价(
A.$25\%$
B.$20\%$
C.$15\%$
B
)。A.$25\%$
B.$20\%$
C.$15\%$
答案:B
解析:
原价为 4800 元,现价为 3840 元。
降价金额为:$4800 - 3840 = 960$(元)。
降价百分比为:$\frac{960}{4800} × 100\% = 20\%$。
降价金额为:$4800 - 3840 = 960$(元)。
降价百分比为:$\frac{960}{4800} × 100\% = 20\%$。
(2)某车间上半月完成全月计划产量的$\frac{1}{2}$,下半月完成计划产量的$75\%$,这个月增产(
A.$20\%$
B.$25\%$
C.$30\%$
B
)。A.$20\%$
B.$25\%$
C.$30\%$
答案:B
解析:
全月计划产量看作单位"1",上半月完成$\frac{1}{2}$,下半月完成$75\%=\frac{3}{4}$,实际完成总量为$\frac{1}{2}+\frac{3}{4}=\frac{5}{4}$。超产比例为$\frac{5}{4}-1=\frac{1}{4}=25\%$。
(3)第一小组和第二小组用糖水做实验(如图)。这两组比较,可知(

A.第一小组的糖水更甜
B.第二小组的糖水更甜
C.一样甜
B
)。
A.第一小组的糖水更甜
B.第二小组的糖水更甜
C.一样甜
答案:B
解析:
计算第一小组糖水的含糖率:
糖的质量是4克,水的质量是70克,糖水的质量为$4 + 70 = 74$克。
含糖率为$\frac{4}{74}\approx5.4\%$。
计算第二小组糖水的含糖率:
糖的质量是5克,水的质量是80克,糖水的质量为$5 + 80 = 85$克。
含糖率为$\frac{5}{85}\approx5.9\%$。
因为$5.9\%>5.4\%$,所以第二小组的糖水更甜。
糖的质量是4克,水的质量是70克,糖水的质量为$4 + 70 = 74$克。
含糖率为$\frac{4}{74}\approx5.4\%$。
计算第二小组糖水的含糖率:
糖的质量是5克,水的质量是80克,糖水的质量为$5 + 80 = 85$克。
含糖率为$\frac{5}{85}\approx5.9\%$。
因为$5.9\%>5.4\%$,所以第二小组的糖水更甜。