(1)$\frac {3}{4}立方米= $(
250 毫升$=$(
750
)立方分米= (750
)升250 毫升$=$(
0.25
)升答案:750,750,0.25
解析:
1立方米=1000立方分米,$\frac{3}{4}×1000 = 750$,所以$\frac{3}{4}$立方米=750立方分米;1立方分米=1升,所以750立方分米=750升。1升=1000毫升,250÷1000=0.25,所以250毫升=0.25升。
(2)6 的倒数是(
$\frac{1}{6}$
);($\frac{3}{5}$
)与$\frac {5}{3}$互为倒数。答案:(2)$\frac{1}{6}$;$\frac{3}{5}$
解析:
1. 根据倒数的定义,一个数 $a$ 的倒数是 $\frac{1}{a}$,所以6的倒数为 $\frac{1}{6}$。
2. 设某数 $x$ 与 $\frac{5}{3}$ 互为倒数,即 $x × \frac{5}{3} = 1$,解得 $x = \frac{3}{5}$。
2. 设某数 $x$ 与 $\frac{5}{3}$ 互为倒数,即 $x × \frac{5}{3} = 1$,解得 $x = \frac{3}{5}$。
(3)在$〇$里填“$>$”“$<$”或“$=$”。
$\frac {9}{11}×24$$◯$$\frac {9}{11}$ $5÷8$$◯$$62.5\%$
$36÷\frac {2}{7}$$◯$$36$ $\frac {2}{13}÷\frac {9}{4}$$◯$$\frac {2}{13}$
$\frac {9}{11}×24$$◯$$\frac {9}{11}$ $5÷8$$◯$$62.5\%$
$36÷\frac {2}{7}$$◯$$36$ $\frac {2}{13}÷\frac {9}{4}$$◯$$\frac {2}{13}$
答案:>;=;>;<
解析:
1. 对于$\frac{9}{11} × 24$和$\frac{9}{11}$的比较:
一个数(0除外)乘大于1的数,积比原数大。
因为$24\gt1$,所以$\frac{9}{11} × 24\gt\frac{9}{11}$。
2. 对于$5÷8$和$62.5\%$的比较:
先计算$5÷8 = 5÷8=\frac{5}{8}=0.625$,而$62.5\% = 0.625$,所以$5÷8 = 62.5\%$。
3. 对于$36÷\frac{2}{7}$和$36$的比较:
一个数(0除外)除以小于1的数,商比原数大。
因为$\frac{2}{7}\lt1$,所以$36÷\frac{2}{7}\gt36$。
4. 对于$\frac{2}{13}÷\frac{9}{4}$和$\frac{2}{13}$的比较:
一个数(0除外)除以大于1的数,商比原数小。
因为$\frac{9}{4}\gt1$,所以$\frac{2}{13}÷\frac{9}{4}\lt\frac{2}{13}$。
一个数(0除外)乘大于1的数,积比原数大。
因为$24\gt1$,所以$\frac{9}{11} × 24\gt\frac{9}{11}$。
2. 对于$5÷8$和$62.5\%$的比较:
先计算$5÷8 = 5÷8=\frac{5}{8}=0.625$,而$62.5\% = 0.625$,所以$5÷8 = 62.5\%$。
3. 对于$36÷\frac{2}{7}$和$36$的比较:
一个数(0除外)除以小于1的数,商比原数大。
因为$\frac{2}{7}\lt1$,所以$36÷\frac{2}{7}\gt36$。
4. 对于$\frac{2}{13}÷\frac{9}{4}$和$\frac{2}{13}$的比较:
一个数(0除外)除以大于1的数,商比原数小。
因为$\frac{9}{4}\gt1$,所以$\frac{2}{13}÷\frac{9}{4}\lt\frac{2}{13}$。
(4)(
15
)÷20= 3÷4= $\frac {24}{(32
)}$= (6
):8= (75
)\%答案:$15$,$32$,$6$,$75$(按顺序填写答案对应位置的内容)分别对应(横线从左到右) ,由于是填空形式按照顺序答案为【15】、【32】、【6】、【75】。
解析:
本题可根据商不变的性质、分数的基本性质、比与分数和除法的关系以及百分数的计算来求解。
求$( )÷20$中的被除数:
根据商不变的性质:被除数和除数同时乘或除以相同的数($0$除外),商不变。
已知$3÷4=( )÷20$,除数由$4$变为$20$,$20÷4 = 5$,即除数乘$5$,那么被除数也要乘$5$,$3×5 = 15$,所以$15÷20 = 3÷4$。
求$\frac{24}{( )}$中的分母:
根据分数的基本性质:分数的分子和分母同时乘或者除以一个相同的数($0$除外),分数的大小不变。
已知$3÷4=\frac{24}{( )}$,$3$变为$24$,$24÷3 = 8$,即分子乘$8$,那么分母也要乘$8$,$4×8 = 32$,所以$\frac{24}{32}=3÷4$。
求$( ):8$中的前项:
根据比与除法的关系$a÷ b = a:b$($b\neq0$),$3÷4 = 3:4$。
再根据比的基本性质:比的前项和后项同时乘或除以相同的数($0$除外),比值不变。
比的后项由$4$变为$8$,$8÷4 = 2$,即后项乘$2$,那么前项也要乘$2$,$3×2 = 6$,所以$6:8 = 3÷4$。
求$( )\%$中的百分数:
计算$3÷4 = 0.75$,把$0.75$转化为百分数,将$0.75$的小数点向右移动两位,再加上百分号,即$0.75 = 75\%$。
求$( )÷20$中的被除数:
根据商不变的性质:被除数和除数同时乘或除以相同的数($0$除外),商不变。
已知$3÷4=( )÷20$,除数由$4$变为$20$,$20÷4 = 5$,即除数乘$5$,那么被除数也要乘$5$,$3×5 = 15$,所以$15÷20 = 3÷4$。
求$\frac{24}{( )}$中的分母:
根据分数的基本性质:分数的分子和分母同时乘或者除以一个相同的数($0$除外),分数的大小不变。
已知$3÷4=\frac{24}{( )}$,$3$变为$24$,$24÷3 = 8$,即分子乘$8$,那么分母也要乘$8$,$4×8 = 32$,所以$\frac{24}{32}=3÷4$。
求$( ):8$中的前项:
根据比与除法的关系$a÷ b = a:b$($b\neq0$),$3÷4 = 3:4$。
再根据比的基本性质:比的前项和后项同时乘或除以相同的数($0$除外),比值不变。
比的后项由$4$变为$8$,$8÷4 = 2$,即后项乘$2$,那么前项也要乘$2$,$3×2 = 6$,所以$6:8 = 3÷4$。
求$( )\%$中的百分数:
计算$3÷4 = 0.75$,把$0.75$转化为百分数,将$0.75$的小数点向右移动两位,再加上百分号,即$0.75 = 75\%$。
(5)$2:0.16$的最简整数比是(
25:2
),比值是(12.5
)。答案:25:2,12.5
解析:
2:0.16=(2×100):(0.16×100)=200:16=(200÷8):(16÷8)=25:2;25:2=25÷2=12.5
(6)六(3)班有 50 名学生,今天实到 48 人,六(3)班今天的出勤率是(
96
)%。答案:96
解析:
出勤率是指实到人数除以应到人数再乘以100%,即 $ \frac{48}{50} × 100\% = 96\% $。
(7)右图是一个长方体纸盒相交于同一顶点的三条棱的长度,这个长方体左侧面的面积是(
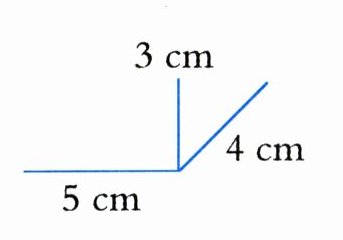
12
)平方厘米;制作出这样一个包装盒,这个包装盒所占的空间是(60
)立方厘米。
答案:12;60
解析:
长方体相交于同一顶点的三条棱分别为长、宽、高,由图可知长=5cm,宽=4cm,高=3cm。左侧面面积=宽×高=4×3=12平方厘米;所占空间即体积=长×宽×高=5×4×3=60立方厘米。
(8)3 个棱长为 1 厘米的正方体拼成一个长方体,它的表面积是(
14
)平方厘米。答案:14
解析:
3个棱长1厘米的正方体拼成长方体,长3厘米、宽1厘米、高1厘米。表面积:(3×1+3×1+1×1)×2=14平方厘米。
(9)$\frac {3}{5}吨的大豆可以榨油\frac {9}{100}$吨,榨 1 吨油需要(
$\frac{20}{3}$
)吨大豆,1 吨大豆可以榨油($\frac{3}{20}$
)吨。答案:$\frac{20}{3}$(或填对应选项)、$\frac{3}{20}$(或填对应选项)
解析:
本题可根据已知条件,通过除法运算分别求出榨$1$吨油需要的大豆吨数以及$1$吨大豆的榨油量。
步骤一:求榨$1$吨油需要多少吨大豆
已知$\frac{3}{5}$吨的大豆可以榨油$\frac{9}{100}$吨,要求榨$1$吨油需要的大豆吨数,就是求大豆的吨数与油的吨数的比值,用大豆的吨数除以油的吨数即可。
所以榨$1$吨油需要的大豆为:$\frac{3}{5}÷\frac{9}{100}=\frac{3}{5}×\frac{100}{9}=\frac{20}{3}$(吨)
步骤二:求$1$吨大豆可以榨多少吨油
要求$1$吨大豆的榨油量,就是求油的吨数与大豆的吨数的比值,用油的吨数除以大豆的吨数即可。
所以$1$吨大豆可以榨油:$\frac{9}{100}÷\frac{3}{5}=\frac{9}{100}×\frac{5}{3}=\frac{3}{20}$(吨)
步骤一:求榨$1$吨油需要多少吨大豆
已知$\frac{3}{5}$吨的大豆可以榨油$\frac{9}{100}$吨,要求榨$1$吨油需要的大豆吨数,就是求大豆的吨数与油的吨数的比值,用大豆的吨数除以油的吨数即可。
所以榨$1$吨油需要的大豆为:$\frac{3}{5}÷\frac{9}{100}=\frac{3}{5}×\frac{100}{9}=\frac{20}{3}$(吨)
步骤二:求$1$吨大豆可以榨多少吨油
要求$1$吨大豆的榨油量,就是求油的吨数与大豆的吨数的比值,用油的吨数除以大豆的吨数即可。
所以$1$吨大豆可以榨油:$\frac{9}{100}÷\frac{3}{5}=\frac{9}{100}×\frac{5}{3}=\frac{3}{20}$(吨)
(10)27 的$\frac {2}{9}$是一个数的$\frac {3}{4}$,这个数是(
8
)。答案:(这里假设选项中正确答案对应的内容为8 ) 填对应选项
解析:
首先计算27的$\frac{2}{9}$,即$27×\frac{2}{9}=6$。设这个数为$x$,则$\frac{3}{4}x = 6$,解得$x = 6÷\frac{3}{4}=6×\frac{4}{3}=8$。
(11)2021 年 3 月,王阿姨购买了 5000 元三年期的国债券,年利率是 4%,三年后一共可得(
5600
)元。答案:5600
解析:
利息=本金×年利率×时间=5000×4%×3=600元,一共可得金额=本金+利息=5000+600=5600元
2 判断题。(对的画“√”,错的画“×”)(共 5 分)
(1)因为$\frac {1}{4}= 25\%$,所以$\frac {1}{4}米= 25\%$米。 (
(2)一个数(零除外)的倒数一定比这个数小。 (
(3)$a和b$都是非零自然数,已知$a×\frac {7}{9}= b÷\frac {7}{9}$,则$a>b$。 (
(4)学校栽的 120 棵柏树全部成活,这批树的成活率是 120%。 (
(5)比的前项加上 12,后项也要加上 12,比值才不会变化。 (
(1)因为$\frac {1}{4}= 25\%$,所以$\frac {1}{4}米= 25\%$米。 (
×
)(2)一个数(零除外)的倒数一定比这个数小。 (
×
)(3)$a和b$都是非零自然数,已知$a×\frac {7}{9}= b÷\frac {7}{9}$,则$a>b$。 (
√
)(4)学校栽的 120 棵柏树全部成活,这批树的成活率是 120%。 (
×
)(5)比的前项加上 12,后项也要加上 12,比值才不会变化。 (
×
)答案:(1)×;(2)×;(3)√;(4)×;(5)×
解析:
(1)百分数表示一个数是另一个数的百分之几,它后面不能接单位名称。米是长度单位,$\frac{1}{4}$米是具体的长度,而$25\%$不能表示具体的长度,所以该说法错误。
(2)真分数的倒数比这个数大,例如$\frac{1}{2}$的倒数是$2$,$2\gt\frac{1}{2}$,所以“一个数(零除外)的倒数一定比这个数小”说法错误。
(3)由$a×\frac{7}{9}=b÷\frac{7}{9}$,可得$a×\frac{7}{9}=b×\frac{9}{7}$,根据比例的基本性质可得$a:b=\frac{9}{7}:\frac{7}{9}=81:49$,所以$a\gt b$,该说法正确。
(4)成活率$=\frac{成活的棵数}{总棵数}×100\%$,$120$棵柏树全部成活,成活率为$\frac{120}{120}×100\% = 100\%$,不可能超过$100\%$,所以该说法错误。
(5)比的基本性质是比的前项和后项同时乘或除以相同的数($0$除外),比值不变,而不是前项和后项同时加上相同的数,比值不变,例如$6:2 = 3$,前项加上$12$变为$18$,后项加上$12$变为$14$,$18:14=\frac{9}{7}\neq3$,所以该说法错误。
(2)真分数的倒数比这个数大,例如$\frac{1}{2}$的倒数是$2$,$2\gt\frac{1}{2}$,所以“一个数(零除外)的倒数一定比这个数小”说法错误。
(3)由$a×\frac{7}{9}=b÷\frac{7}{9}$,可得$a×\frac{7}{9}=b×\frac{9}{7}$,根据比例的基本性质可得$a:b=\frac{9}{7}:\frac{7}{9}=81:49$,所以$a\gt b$,该说法正确。
(4)成活率$=\frac{成活的棵数}{总棵数}×100\%$,$120$棵柏树全部成活,成活率为$\frac{120}{120}×100\% = 100\%$,不可能超过$100\%$,所以该说法错误。
(5)比的基本性质是比的前项和后项同时乘或除以相同的数($0$除外),比值不变,而不是前项和后项同时加上相同的数,比值不变,例如$6:2 = 3$,前项加上$12$变为$18$,后项加上$12$变为$14$,$18:14=\frac{9}{7}\neq3$,所以该说法错误。