1. 填空题。
(1)用两个(
(2)一个三角形的底边长是 12 cm,底边上的高是 4 cm,它的面积是(
(1)用两个(
完全一样
)的三角形可以拼出一个平行四边形,平行四边形的面积等于原来三角形面积的(2倍
),平行四边形的底和高分别等于原三角形的(底和高
),所以三角形的面积= ($\frac{1}{2}$×底×高
),用字母表示是($S = ah÷2$
)。(2)一个三角形的底边长是 12 cm,底边上的高是 4 cm,它的面积是(
24
)$cm^2,$与它等底等高的平行四边形的面积是(48
)$cm^2。$答案:(1)答案依次为:完全一样;2倍;底和高;$\frac{1}{2}$×底×高;$S = ah÷2$;
(2)答案依次为:24;48。
(2)答案依次为:24;48。
解析:
(1)
两个完全一样的三角形可以拼成一个平行四边形,通过实际操作可知,拼成的平行四边形的面积等于原来三角形面积的2倍;平行四边形的底就是三角形的底,平行四边形的高就是三角形的高。
因为平行四边形面积公式为$S = ah$($a$表示底,$h$表示高),那么三角形面积是平行四边形面积的一半,所以三角形面积$S=\frac{1}{2}ah$,用字母表示是$S = ah÷2$。
(2)
已知三角形底$a = 12cm$,高$h = 4cm$,根据三角形面积公式$S=\frac{1}{2}ah$,可得$S=\frac{1}{2}×12×4 = 24cm^{2}$。
因为平行四边形面积是与它等底等高三角形面积的2倍,所以平行四边形面积为$24×2 = 48cm^{2}$。
两个完全一样的三角形可以拼成一个平行四边形,通过实际操作可知,拼成的平行四边形的面积等于原来三角形面积的2倍;平行四边形的底就是三角形的底,平行四边形的高就是三角形的高。
因为平行四边形面积公式为$S = ah$($a$表示底,$h$表示高),那么三角形面积是平行四边形面积的一半,所以三角形面积$S=\frac{1}{2}ah$,用字母表示是$S = ah÷2$。
(2)
已知三角形底$a = 12cm$,高$h = 4cm$,根据三角形面积公式$S=\frac{1}{2}ah$,可得$S=\frac{1}{2}×12×4 = 24cm^{2}$。
因为平行四边形面积是与它等底等高三角形面积的2倍,所以平行四边形面积为$24×2 = 48cm^{2}$。
2. 计算下面各三角形的面积。
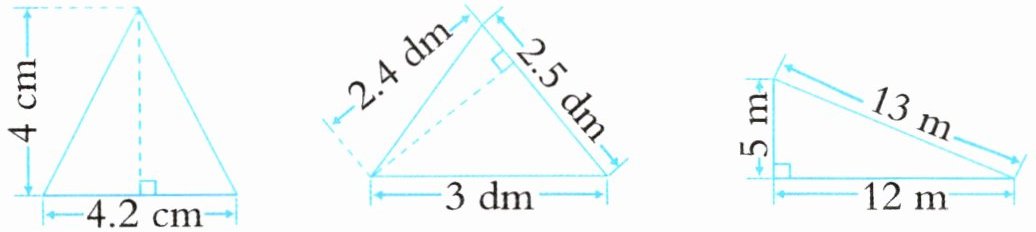

答案:1. 底=4.2cm,高=4cm
面积=4.2×4÷2=8.4cm²
2. 底=2.5dm,高=2.4dm
面积=2.5×2.4÷2=3dm²
3. 底=12m,高=5m
面积=12×5÷2=30m²
面积=4.2×4÷2=8.4cm²
2. 底=2.5dm,高=2.4dm
面积=2.5×2.4÷2=3dm²
3. 底=12m,高=5m
面积=12×5÷2=30m²
解析:
$S=\frac{1}{2}×4.2×4=8.4\ cm^2$
$S=\frac{1}{2}×2.4×2.5=3\ dm^2$
$S=\frac{1}{2}×12×5=30\ m^2$
$S=\frac{1}{2}×2.4×2.5=3\ dm^2$
$S=\frac{1}{2}×12×5=30\ m^2$
3.
|图形|底/cm|高/cm|面积$/cm^2$|
| | | |估算|计算|
|平行四边形|12.5|8.4|
|三角形|7.8|5|

|图形|底/cm|高/cm|面积$/cm^2$|
| | | |估算|计算|
|平行四边形|12.5|8.4|
104
|105
||三角形|7.8|5|
20
|19.5
|
答案:对于平行四边形:
估算:$12.5\approx13, 8.4\approx8$,$13×8 = 104$,面积估算为$104cm^{2}$。
计算:根据平行四边形面积公式$S = a× h$($a$为底,$h$为高),$S=12.5×8.4 = 105cm^{2}$。
对于三角形:
估算:$7.8\approx8$,$8×5÷2 = 20$,面积估算为$20cm^{2}$。
计算:根据三角形面积公式$S = a× h÷2$($a$为底,$h$为高),$S = 7.8×5÷2=19.5cm^{2}$。
|图形|底/cm|高/cm|面积$/cm^2$|\\
| ---- | ---- | ---- | ---- | ---- |
| | | |估算|计算|\\
|平行四边形|12.5|8.4|104|105|\\
|三角形|7.8|5|20|19.5|
估算:$12.5\approx13, 8.4\approx8$,$13×8 = 104$,面积估算为$104cm^{2}$。
计算:根据平行四边形面积公式$S = a× h$($a$为底,$h$为高),$S=12.5×8.4 = 105cm^{2}$。
对于三角形:
估算:$7.8\approx8$,$8×5÷2 = 20$,面积估算为$20cm^{2}$。
计算:根据三角形面积公式$S = a× h÷2$($a$为底,$h$为高),$S = 7.8×5÷2=19.5cm^{2}$。
|图形|底/cm|高/cm|面积$/cm^2$|\\
| ---- | ---- | ---- | ---- | ---- |
| | | |估算|计算|\\
|平行四边形|12.5|8.4|104|105|\\
|三角形|7.8|5|20|19.5|
4. 先估测下面各三角形的面积,再测量并计算面积。

估测的值是
估测的值是

估测的值是
4(答案不唯一,合理即可)
。估测的值是
10(答案不唯一,合理即可)
。答案:第一个三角形:
估测的值是$4$(答案不唯一,合理即可)
计算:
底边长$3$厘米,高$2$厘米,
面积$ = \frac{1}{2} × 3 × 2 = 3$(平方厘米)
第二个三角形:
估测的值是$10$(答案不唯一,合理即可)
计算:
底边长$4$厘米,高$3$厘米,
面积$ = \frac{1}{2} × 4 × 3 = 6$(平方厘米)
估测的值是$4$(答案不唯一,合理即可)
计算:
底边长$3$厘米,高$2$厘米,
面积$ = \frac{1}{2} × 3 × 2 = 3$(平方厘米)
第二个三角形:
估测的值是$10$(答案不唯一,合理即可)
计算:
底边长$4$厘米,高$3$厘米,
面积$ = \frac{1}{2} × 4 × 3 = 6$(平方厘米)