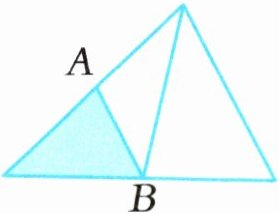
1 下图中大三角形的面积是$20 cm^2,A、$B分别是所在边的中点。求涂色部分的面积。
答案：5 cm²
解析：
连接大三角形顶点与B点，形成四个等底等高的小三角形，每个小三角形面积为$20÷4 = 5\,cm^2$，涂色部分为其中一个小三角形，面积为$5\,cm^2$。
$5\,cm^2$
$5\,cm^2$
2 下图中涂色部分的面积是$6 cm^2,$三角形ABC的面积是多少平方厘米?
答案：15 cm²
解析：
设涂色部分三角形的高为$h$ cm。
涂色部分面积：$\frac{1}{2} × 2 × h = 6$，解得$h = 6$。
三角形ABC的底为$3 + 2 = 5$ cm，高为$h = 6$ cm。
面积：$\frac{1}{2} × 5 × 6 = 15$ $cm^2$。
15
涂色部分面积：$\frac{1}{2} × 2 × h = 6$，解得$h = 6$。
三角形ABC的底为$3 + 2 = 5$ cm，高为$h = 6$ cm。
面积：$\frac{1}{2} × 5 × 6 = 15$ $cm^2$。
15
一个等腰直角三角形的斜边长是8 cm,求这个等腰直角三角形的面积。
用几个这样的三角形试着拼一拼。
用几个这样的三角形试着拼一拼。
答案：16 cm²
解析：
将两个这样的等腰直角三角形斜边重合，可拼成一个边长为8 cm的正方形。
该正方形面积为$8×8 = 64\ cm^2$，
故一个等腰直角三角形面积为$64÷2 = 32\ cm^2$。
1
该正方形面积为$8×8 = 64\ cm^2$，
故一个等腰直角三角形面积为$64÷2 = 32\ cm^2$。
1