1 一个梯形的面积是 $216dm^{2}$,它的上底是 $15dm$,高是 $16dm$,这个梯形的下底是多少分米？(列方程解决。)
答案：设下底为 $x 分米$。
根据梯形面积公式，$面积 = \frac{1}{2} × (上底 + 下底) × 高$，
代入已知数值，得：
$216 = \frac{1}{2} × (15 + x) × 16$，
$216 = 8 × (15 + x)$，
$216 = 120 + 8x$，
$8x = 96$，
$x = 12$。
答：这个梯形的下底是$12dm$。
根据梯形面积公式，$面积 = \frac{1}{2} × (上底 + 下底) × 高$，
代入已知数值，得：
$216 = \frac{1}{2} × (15 + x) × 16$，
$216 = 8 × (15 + x)$，
$216 = 120 + 8x$，
$8x = 96$，
$x = 12$。
答：这个梯形的下底是$12dm$。
2 如图,有一块直角梯形的地,它的下底是 $40m$。如果上底增加 $28m$,这块地就变成了正方形,原来直角梯形的面积是多少平方米？
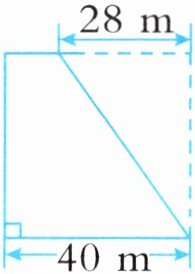
答案：1. 首先求梯形的高和上底：
已知下底$b = 40m$，上底增加$28m$后变成正方形，那么梯形的高$h$等于正方形的边长，即$h = 40m$。
原来梯形的上底$a=40 - 28=12m$。
2. 然后根据梯形面积公式$S=(a + b)h÷2$计算面积：
把$a = 12m$，$b = 40m$，$h = 40m$代入公式，可得$S=(12 + 40)×40÷2$
先算括号里的$12+40 = 52$，再算$52×40 = 2080$，最后$2080÷2=1040$（平方米）。
答：原来直角梯形的面积是$1040$平方米。
已知下底$b = 40m$，上底增加$28m$后变成正方形，那么梯形的高$h$等于正方形的边长，即$h = 40m$。
原来梯形的上底$a=40 - 28=12m$。
2. 然后根据梯形面积公式$S=(a + b)h÷2$计算面积：
把$a = 12m$，$b = 40m$，$h = 40m$代入公式，可得$S=(12 + 40)×40÷2$
先算括号里的$12+40 = 52$，再算$52×40 = 2080$，最后$2080÷2=1040$（平方米）。
答：原来直角梯形的面积是$1040$平方米。
在下面的等腰梯形中,你能找到几组面积相等的三角形？
答案：1. △ABC与△DBC：同底BC，等高（A、D到BC距离相等），面积相等。
2. △ABD与△ACD：同底AD，等高（B、C到AD距离相等），面积相等。
3. △AOB与△COD：△ABC与△DBC面积相等，均减去公共部分△BOC，剩余部分面积相等。
结论：3组。
2. △ABD与△ACD：同底AD，等高（B、C到AD距离相等），面积相等。
3. △AOB与△COD：△ABC与△DBC面积相等，均减去公共部分△BOC，剩余部分面积相等。
结论：3组。
1 判断题。(对的画“√”,错的画“×”。)
(1)只有一组对边平行的四边形叫作梯形。(
(2)如果梯形的上底和下底都扩大到原来的 $2$ 倍,高不变,面积就扩大到原来的 $4$ 倍。(
(3)两个完全一样的直角梯形可以拼成一个长方形。(
(4)梯形的面积等于平行四边形面积的一半。(
(5)梯形可以分成两个平行四边形。(
(1)只有一组对边平行的四边形叫作梯形。(
√
)(2)如果梯形的上底和下底都扩大到原来的 $2$ 倍,高不变,面积就扩大到原来的 $4$ 倍。(
×
)(3)两个完全一样的直角梯形可以拼成一个长方形。(
√
)(4)梯形的面积等于平行四边形面积的一半。(
×
)(5)梯形可以分成两个平行四边形。(
×
)答案：(1)√
(2)×
(3)√
(4)×
(5)×
(2)×
(3)√
(4)×
(5)×
解析：
(1) 根据梯形的定义，只有一组对边平行的四边形是梯形，该说法符合梯形定义，所以正确。
(2) 梯形面积公式为$S=(a + b)h÷2$（$a$、$b$为上底和下底，$h$为高），上底和下底都扩大到原来的$2$倍，新的面积$S'=(2a + 2b)h÷2=2(a + b)h÷2 = 2S$，面积扩大到原来的$2$倍，不是$4$倍，所以该说法错误。
(3) 两个完全一样的直角梯形，将其中一个翻转，使它们的斜边相接，就可以拼成一个长方形，所以该说法正确。
(4) 梯形面积$S=(a + b)h÷2$，平行四边形面积$S = base× height$（$base$为底，$height$为高），只有在特定条件下梯形面积才是平行四边形面积的一半，并不是所有梯形面积都等于平行四边形面积的一半，所以该说法错误。
(5) 梯形是一组对边平行，平行四边形是两组对边分别平行，梯形不能分成两个平行四边形，所以该说法错误。
(2) 梯形面积公式为$S=(a + b)h÷2$（$a$、$b$为上底和下底，$h$为高），上底和下底都扩大到原来的$2$倍，新的面积$S'=(2a + 2b)h÷2=2(a + b)h÷2 = 2S$，面积扩大到原来的$2$倍，不是$4$倍，所以该说法错误。
(3) 两个完全一样的直角梯形，将其中一个翻转，使它们的斜边相接，就可以拼成一个长方形，所以该说法正确。
(4) 梯形面积$S=(a + b)h÷2$，平行四边形面积$S = base× height$（$base$为底，$height$为高），只有在特定条件下梯形面积才是平行四边形面积的一半，并不是所有梯形面积都等于平行四边形面积的一半，所以该说法错误。
(5) 梯形是一组对边平行，平行四边形是两组对边分别平行，梯形不能分成两个平行四边形，所以该说法错误。
|上底/m|下底/m|高/m|面积/m^2|
| $3.5$ | $6.8$ | $4$ |
| $2.1$ | $6.5$ | $3$ |
| $4.8$ | $6$ | $4$ |
| $3.5$ | $6.8$ | $4$ |
20.6
|| $2.1$ | $6.5$ | $3$ |
12.9
|| $4.8$ | $6$ | $4$ |
21.6
|答案：|上底/m|下底/m|高/m|面积/$m^2$|
| ---- | ---- | ---- | ---- |
|3.5|6.8|4|20.6|
|2.1|6.5|3|12.9|
|4.8|6|4|21.6|
| ---- | ---- | ---- | ---- |
|3.5|6.8|4|20.6|
|2.1|6.5|3|12.9|
|4.8|6|4|21.6|
解析：
梯形的面积公式为$S=(a+b)h÷2$（其中$S$表示面积，$a$表示上底，$b$表示下底，$h$表示高）。
对于第一组数据，$a = 3.5m$，$b = 6.8m$，$h = 4m$，则$S=(3.5 + 6.8)×4÷2=10.3×4÷2 = 20.6m^{2}$。
对于第二组数据，$a = 2.1m$，$b = 6.5m$，$h = 3m$，则$S=(2.1 + 6.5)×3÷2=8.6×3÷2 = 12.9m^{2}$。
对于第三组数据，$a = 4.8m$，$b = 6m$，$h = 4m$，则$S=(4.8 + 6)×4÷2=10.8×4÷2 = 21.6m^{2}$。
对于第一组数据，$a = 3.5m$，$b = 6.8m$，$h = 4m$，则$S=(3.5 + 6.8)×4÷2=10.3×4÷2 = 20.6m^{2}$。
对于第二组数据，$a = 2.1m$，$b = 6.5m$，$h = 3m$，则$S=(2.1 + 6.5)×3÷2=8.6×3÷2 = 12.9m^{2}$。
对于第三组数据，$a = 4.8m$，$b = 6m$，$h = 4m$，则$S=(4.8 + 6)×4÷2=10.8×4÷2 = 21.6m^{2}$。
3 解决问题。
(1)下图是一个拦河坝的横截面图,求这个拦河坝横截面的实际面积。
(2)一个梯形的果园,上底是 $160m$,下底是 $180m$,高是 $50m$。如果每棵果树约占地 $10m^{2}$,这个果园约有果树多少棵？
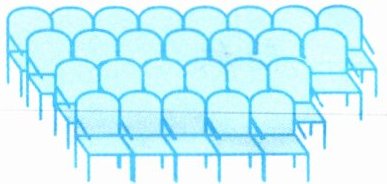
(3)计算下图所示的小放映厅一共有多少个座位。
(4)下图所示是一个梯形鱼塘,面积是 $759m^{2}$。如果要从上底到下底拉一条电线,这条电线至少是多少米？
(1)下图是一个拦河坝的横截面图,求这个拦河坝横截面的实际面积。
(2)一个梯形的果园,上底是 $160m$,下底是 $180m$,高是 $50m$。如果每棵果树约占地 $10m^{2}$,这个果园约有果树多少棵？
(3)计算下图所示的小放映厅一共有多少个座位。
(4)下图所示是一个梯形鱼塘,面积是 $759m^{2}$。如果要从上底到下底拉一条电线,这条电线至少是多少米？
答案：(1)
梯形面积公式$S=(a + b)h÷2$（$a$为上底，$b$为下底，$h$为高），此梯形上底$2.4m$，下底$10m$，高$3m$。
$S=(2.4 + 10)×3÷2=18.6$（$m^{2}$）
答：这个拦河坝横截面的实际面积是$18.6m^{2}$。
(2)
先根据梯形面积公式求果园面积：$S=(160 + 180)×50÷2 = 8500$（$m^{2}$）
每棵果树约占地$10m^{2}$，则果树数量为$8500÷10 = 850$（棵）
答：这个果园约有果树$850$棵。
(3)
前$4$排座位数：$1+3+5+7 = 16$（个）
中间$6$排每排$9$个，共$6×9 = 54$个
后$3$排座位数：$11+13+15 = 39$（个）
总座位数：$16+54+39 = 109$（个）
答：小放映厅一共有$109$个座位。
(4)
根据梯形面积公式$S=(a + b)h÷2$，已知$S = 759m^{2}$，$a = 21m$，$b = 45m$，求高$h$。
$h=2S÷(a + b)=2×759÷(21 + 45)=23$（$m$）
答：这条电线至少是$23$米。
梯形面积公式$S=(a + b)h÷2$（$a$为上底，$b$为下底，$h$为高），此梯形上底$2.4m$，下底$10m$，高$3m$。
$S=(2.4 + 10)×3÷2=18.6$（$m^{2}$）
答：这个拦河坝横截面的实际面积是$18.6m^{2}$。
(2)
先根据梯形面积公式求果园面积：$S=(160 + 180)×50÷2 = 8500$（$m^{2}$）
每棵果树约占地$10m^{2}$，则果树数量为$8500÷10 = 850$（棵）
答：这个果园约有果树$850$棵。
(3)
前$4$排座位数：$1+3+5+7 = 16$（个）
中间$6$排每排$9$个，共$6×9 = 54$个
后$3$排座位数：$11+13+15 = 39$（个）
总座位数：$16+54+39 = 109$（个）
答：小放映厅一共有$109$个座位。
(4)
根据梯形面积公式$S=(a + b)h÷2$，已知$S = 759m^{2}$，$a = 21m$，$b = 45m$，求高$h$。
$h=2S÷(a + b)=2×759÷(21 + 45)=23$（$m$）
答：这条电线至少是$23$米。