5 面积计算。(每小题 4 分,共 8 分)
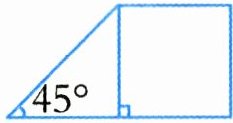
(1)下图中正方形的周长是 $ 28cm $,求梯形的面积。
(2)如图,在梯形 $ ABDE $ 中,$ BC = 10cm $,$ CD = 6cm $,平行四边形 $ ABCE $的面积是 $ 110cm^{2} $,求图中涂色部分的面积。

(1)下图中正方形的周长是 $ 28cm $,求梯形的面积。

(2)如图,在梯形 $ ABDE $ 中,$ BC = 10cm $,$ CD = 6cm $,平行四边形 $ ABCE $的面积是 $ 110cm^{2} $,求图中涂色部分的面积。

答案:(1)
正方形边长:$28÷4 = 7(cm)$
梯形的高与正方形边长相等为$7cm$,梯形上底与下底和:$7 + 7×(1 + 1)=21(cm)$($45^{\circ}$角说明梯形上底与正方形边长相等,下底是正方形边长的$2$倍)
梯形面积:$21×7÷2 = 73.5(cm^{2})$
(2)
平行四边形$ABCE$的底$BC = 10cm$,根据面积公式可得高:$110÷10 = 11(cm)$
涂色部分为三角形,底$CD = 6cm$,高与平行四边形高相同为$11cm$
涂色部分面积:$6×11÷2 = 33(cm^{2})$
正方形边长:$28÷4 = 7(cm)$
梯形的高与正方形边长相等为$7cm$,梯形上底与下底和:$7 + 7×(1 + 1)=21(cm)$($45^{\circ}$角说明梯形上底与正方形边长相等,下底是正方形边长的$2$倍)
梯形面积:$21×7÷2 = 73.5(cm^{2})$
(2)
平行四边形$ABCE$的底$BC = 10cm$,根据面积公式可得高:$110÷10 = 11(cm)$
涂色部分为三角形,底$CD = 6cm$,高与平行四边形高相同为$11cm$
涂色部分面积:$6×11÷2 = 33(cm^{2})$
(1)服装厂选用一种布做上衣,做一件上衣需要布 $ 1.5m $。现有 $ 132m $ 布,可以做多少件上衣? 如果每件上衣卖 92.5 元,这些上衣一共可以卖多少钱?
答案:答题:
1. 可做上衣件数:
$132÷1.5 = 88$(件)
2. 这些上衣可卖总价:
$92.5×88 = 8140$(元)
答:可以做88件上衣,这些上衣一共可以卖8140元。
1. 可做上衣件数:
$132÷1.5 = 88$(件)
2. 这些上衣可卖总价:
$92.5×88 = 8140$(元)
答:可以做88件上衣,这些上衣一共可以卖8140元。
(2)王叔叔昨天去超市带了 58.5 元,买了 $ 2kg $ 苹果,每千克 9 元,剩下的钱买了 $ 1.5kg $ 猪肉,每千克猪肉多少钱?
答案:1. 买苹果花费:$2×9 = 18$(元)
2. 剩余钱数:$58.5 - 18 = 40.5$(元)
3. 猪肉单价:$40.5÷1.5 = 27$(元/千克)
答:每千克猪肉27元。
2. 剩余钱数:$58.5 - 18 = 40.5$(元)
3. 猪肉单价:$40.5÷1.5 = 27$(元/千克)
答:每千克猪肉27元。
(3)客货两车同时从两地相对开出,3 个小时后两车未相遇,且相距 $ 30km $。客车每小时行 $ 72km $,货车每小时行 $ 78km $。两地之间的总路程是多少千米?
答案:解:客车3小时行驶路程:$72×3 = 216$(km)
货车3小时行驶路程:$78×3 = 234$(km)
两地总路程:$216 + 234 + 30 = 480$(km)
答:两地之间的总路程是480千米。
货车3小时行驶路程:$78×3 = 234$(km)
两地总路程:$216 + 234 + 30 = 480$(km)
答:两地之间的总路程是480千米。
(4)一条公路长 $ 300km $,如果在路的一边每隔 $ 50m $ 立一根电线杆,两头都立,一共要准备多少根电线杆?
答案:300km=300000m
间隔数:300000÷50=6000(个)
电线杆数:6000+1=6001(根)
答:一共要准备6001根电线杆。
间隔数:300000÷50=6000(个)
电线杆数:6000+1=6001(根)
答:一共要准备6001根电线杆。