7. 为了检验两条纸带①,②的边线是否平行,小明和小丽采用两种不同的方法:小明将纸带①沿 AB 折叠,量得∠1= ∠2= 50°;小丽将纸带②沿 GH 折叠,发现 GD 与 GC 重合,HF 与 HE 重合.则下列判断正确的是(
A.纸带①的边线平行,纸带②的边线不平行
B.纸带①,②的边线都平行
C.纸带①的边线不平行,纸带②的边线平行
D.纸带①,②的边线都不平行
C
)A.纸带①的边线平行,纸带②的边线不平行
B.纸带①,②的边线都平行
C.纸带①的边线不平行,纸带②的边线平行
D.纸带①,②的边线都不平行
答案:C
解析:
纸带①判断:
折叠后,设∠1的对顶角为∠3,∠2的邻补角为∠4。
∠1=∠2=50°,则∠3=50°,∠4=180°-50°=130°。
因∠3≠∠4,纸带①上下边线被AB所截形成的内错角不相等,故边线不平行。
纸带②判断:
折叠后GD与GC重合,HF与HE重合,得∠DGH=∠CGH,∠FHG=∠EHG。
设∠DGH=∠CGH=α,∠FHG=∠EHG=β,则∠DGC=2α,∠FHE=2β。
因GD//HF(原纸带边缘),∠DGC+∠FHE=180°(同旁内角互补),即2α+2β=180°,得α+β=90°。
折叠线GH与EH所成角∠GHE=β,∠HGC=α,α+β=90°,则∠GHE+∠HGC=90°,即GC//HE(内错角相等)。
又GC、HE分别为纸带上下边线,故边线平行。
结论:纸带①边线不平行,纸带②边线平行。
C
折叠后,设∠1的对顶角为∠3,∠2的邻补角为∠4。
∠1=∠2=50°,则∠3=50°,∠4=180°-50°=130°。
因∠3≠∠4,纸带①上下边线被AB所截形成的内错角不相等,故边线不平行。
纸带②判断:
折叠后GD与GC重合,HF与HE重合,得∠DGH=∠CGH,∠FHG=∠EHG。
设∠DGH=∠CGH=α,∠FHG=∠EHG=β,则∠DGC=2α,∠FHE=2β。
因GD//HF(原纸带边缘),∠DGC+∠FHE=180°(同旁内角互补),即2α+2β=180°,得α+β=90°。
折叠线GH与EH所成角∠GHE=β,∠HGC=α,α+β=90°,则∠GHE+∠HGC=90°,即GC//HE(内错角相等)。
又GC、HE分别为纸带上下边线,故边线平行。
结论:纸带①边线不平行,纸带②边线平行。
C
8. 如图,直线 AB,CD 分别与 EF 相交于点 G,H,已知∠1= 70°,∠2= 70°,判断 AB 与 CD 是否平行,并说明理由.
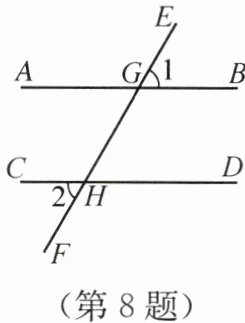

答案:AB//CD.因为∠1=∠AGH,∠1=∠2=70°,所以∠2=∠AGH,所以AB//CD
9. 如图,点 O 在直线 AB 上,OC 平分∠AOF,OD 平分∠BOF,F 是 DE 上一点,连接 OF.
(1)判断 OC 与 OD 是否垂直,并说明理由;
(2)若∠D 与∠1 互余,判断 ED 与 AB 是否平行,并说明理由.

(1)判断 OC 与 OD 是否垂直,并说明理由;
(2)若∠D 与∠1 互余,判断 ED 与 AB 是否平行,并说明理由.

答案:(1)OC⊥OD.因为OC平分∠AOF,OD平分∠BOF,所以∠COF=$\frac{1}{2}$∠AOF,∠DOF=$\frac{1}{2}$∠BOF,因为∠AOF+∠BOF=180°,所以∠COF+∠DOF=$\frac{1}{2}$(∠AOF+∠BOF)=90°,所以OC⊥OD (2)ED//AB.由
(1)知,OC⊥OD,所以∠COD=90°,所以∠1+∠DOB=90°,因为∠D+∠1=90°,所以∠D=∠DOB,所以ED//AB
(1)知,OC⊥OD,所以∠COD=90°,所以∠1+∠DOB=90°,因为∠D+∠1=90°,所以∠D=∠DOB,所以ED//AB