9. 计算:
(1)48°39′+67°31′;
(2)61°39′-22°5′32″;
(3)21°17′×6;
(4)65°24′÷4.
(1)48°39′+67°31′;
(2)61°39′-22°5′32″;
(3)21°17′×6;
(4)65°24′÷4.
答案:(1)48°39'+67°31'=115°70'=116°10' (2)61°39'-22°5'32''=61°38'60''-22°5'32''=39°33'28'' (3)21°17'×6=126°102'=127°42' (4)65°24'÷4=16.25°6'=16°21'
解析:
(1) $48^\circ39'+67^\circ31'=115^\circ70'=116^\circ10'$
(2) $61^\circ39'-22^\circ5'32''=61^\circ38'60''-22^\circ5'32''=39^\circ33'28''$
(3) $21^\circ17'×6=126^\circ102'=127^\circ42'$
(4) $65^\circ24'÷4=16^\circ21'$
10. 如图,O,A,B,C,D都为格点,∠AOB= ∠α,∠COD= ∠β.
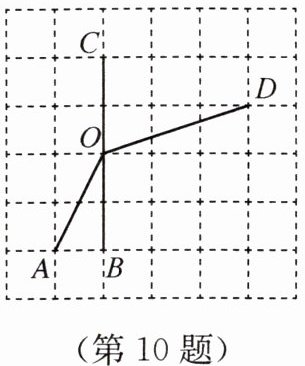
(1)在图中找出一个格点E,连接OE,使得∠DOE= ∠α+∠β;
(2)在图中找出一个格点F,连接OF,使得∠DOF= ∠β-∠α.

(1)在图中找出一个格点E,连接OE,使得∠DOE= ∠α+∠β;
(2)在图中找出一个格点F,连接OF,使得∠DOF= ∠β-∠α.
答案:
如图
如图

11. (1)数学活动课上,李老师让同学们准备一副三角板,并利用它们画出一些角,例如30°,45°,60°,90°. 小明利用三角板画出了一个120°的角. 小乐利用三角板画出了一个15°的角. 你还能用三角板画出多少度的角?
(2)如图,李老师将两个三角板放置在一起,于是产生了新的数学问题. ∠AOB= ∠DCO= 90°,∠A= 45°,∠DOC= 30°,在∠BOD,∠AOC(∠BOD≤180°,∠AOC≤180°)内作射线OP,OQ,且∠POB= 2∠DOP,∠QOA= 2∠QOC. 求∠POQ的度数.

(2)如图,李老师将两个三角板放置在一起,于是产生了新的数学问题. ∠AOB= ∠DCO= 90°,∠A= 45°,∠DOC= 30°,在∠BOD,∠AOC(∠BOD≤180°,∠AOC≤180°)内作射线OP,OQ,且∠POB= 2∠DOP,∠QOA= 2∠QOC. 求∠POQ的度数.

答案:(1)用三角板还能作出75°和105°的角,等等 (2)因为∠AOB=90°,∠COD=30°,所以∠BOD+∠AOC=360°-∠AOB-∠DOC=240°,因为∠POB=2∠DOP,∠QOA=2∠QOC,所以∠DOP= $\frac{1}{3}$∠BOD,∠QOC= $\frac{1}{3}$∠AOC,所以∠DOP+∠QOC= $\frac{1}{3}$(∠BOD+∠AOC)=80°,因为∠POQ=∠DOP+∠QOC+∠COD,∠COD=30°,所以∠POQ=80°+30°=110°
解析:
(1)75°,105°,135°,150°
(2)
∵∠AOB=90°,∠DCO=90°,∠DOC=30°
∴∠BOD+∠AOC=360°-∠AOB-∠DOC=240°
∵∠POB=2∠DOP
∴∠DOP=$\frac{1}{3}$∠BOD
∵∠QOA=2∠QOC
∴∠QOC=$\frac{1}{3}$∠AOC
∴∠DOP+∠QOC=$\frac{1}{3}$(∠BOD+∠AOC)=80°
∵∠POQ=∠DOP+∠QOC+∠DOC
∴∠POQ=80°+30°=110°
(2)
∵∠AOB=90°,∠DCO=90°,∠DOC=30°
∴∠BOD+∠AOC=360°-∠AOB-∠DOC=240°
∵∠POB=2∠DOP
∴∠DOP=$\frac{1}{3}$∠BOD
∵∠QOA=2∠QOC
∴∠QOC=$\frac{1}{3}$∠AOC
∴∠DOP+∠QOC=$\frac{1}{3}$(∠BOD+∠AOC)=80°
∵∠POQ=∠DOP+∠QOC+∠DOC
∴∠POQ=80°+30°=110°