5. 已知正比例函数 $ y_1= k_1x(k_1\neq0) $ 和 $ y_2= k_2x(k_2\neq0) $.当 $ x= 3 $ 时,$ y_1+y_2= 12 $;当 $ x= -2 $ 时,$ y_1-y_2= -10 $.
(1) 求 $ k_1,k_2 $ 的值;
(2) 在同一平面直角坐标系中画出这两个函数的图象;
(3) 根据图象,直接写出当 $ y_1<y_2 $ 时,x的取值范围.
(1) 求 $ k_1,k_2 $ 的值;
(2) 在同一平面直角坐标系中画出这两个函数的图象;
(3) 根据图象,直接写出当 $ y_1<y_2 $ 时,x的取值范围.
答案:答案略
解析:
(1)根据题意得:
$\begin{cases}3k_1 + 3k_2 = 12 \\-2k_1 - (-2k_2) = -10\end{cases}$
化简得:
$\begin{cases}k_1 + k_2 = 4 \\-k_1 + k_2 = -5\end{cases}$
两式相加得:$2k_2=-1$,解得$k_2=-\frac{1}{2}$
将$k_2=-\frac{1}{2}$代入$k_1 + k_2 = 4$,得$k_1=4 - (-\frac{1}{2})=\frac{9}{2}$
所以$k_1=\frac{9}{2}$,$k_2=-\frac{1}{2}$
(2) 函数$y_1=\frac{9}{2}x$过点$(0,0)$和$(2,9)$;函数$y_2=-\frac{1}{2}x$过点$(0,0)$和$(2,-1)$,图象略
(3) $x < 0$
6. 已知正比例函数 $ y= kx(k\neq0) $ 的图象如图所示,在同一平面直角坐标系中画出 $ y= 2kx,y= -kx $ 的图象.
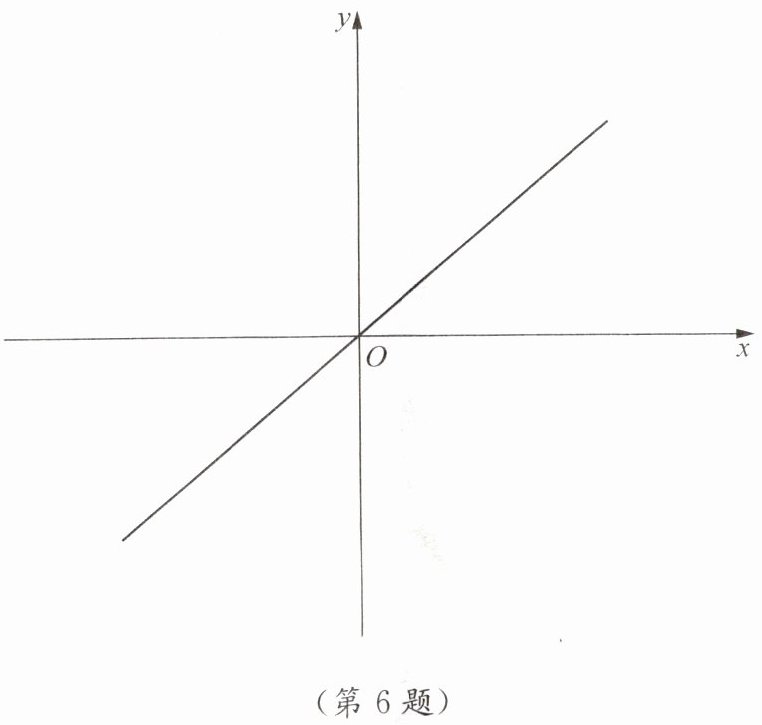

答案:【解析】:
本题考查正比例函数的图像性质。
根据题目给出的正比例函数 $y = kx$($k \neq 0$)的图象,可以判断 $k$ 的正负。
由于图象经过第一、三象限,因此 $k > 0$。
对于函数 $y = 2kx$:
由于 $k > 0$,则 $2k > 0$,因此函数 $y = 2kx$ 的图象也是一条经过第一、三象限的直线,且斜率比 $y = kx$ 更陡。
对于函数 $y = -kx$:
由于 $k > 0$,则 $-k < 0$,因此函数 $y = -kx$ 的图象是一条经过第二、四象限的直线。
【答案】:
图略。
本题考查正比例函数的图像性质。
根据题目给出的正比例函数 $y = kx$($k \neq 0$)的图象,可以判断 $k$ 的正负。
由于图象经过第一、三象限,因此 $k > 0$。
对于函数 $y = 2kx$:
由于 $k > 0$,则 $2k > 0$,因此函数 $y = 2kx$ 的图象也是一条经过第一、三象限的直线,且斜率比 $y = kx$ 更陡。
对于函数 $y = -kx$:
由于 $k > 0$,则 $-k < 0$,因此函数 $y = -kx$ 的图象是一条经过第二、四象限的直线。
【答案】:
图略。