5. 已知一次函数$y= kx+b的图象经过点(2,-1)和(-1,5)$.
(1) 求$k$,$b$的值;
(2) 画出该一次函数的图象,并说明函数图象可由正比例函数$y= kx$的图象如何平移得到.
(1) 求$k$,$b$的值;
(2) 画出该一次函数的图象,并说明函数图象可由正比例函数$y= kx$的图象如何平移得到.
答案:【解析】:
本题主要考查一次函数的性质,包括求解一次函数的表达式以及函数图象的平移。
(1) 对于求$k$和$b$的值,我们可以将给定的两个点$(2,-1)$和$(-1,5)$代入一次函数$y=kx+b$,得到两个方程,然后解这个方程组来找到$k$和$b$的值。
(2) 对于画出函数图象,我们需要先找到函数与坐标轴的交点,然后连接这些点来绘制函数图象。接着,我们可以通过比较一次函数$y=kx+b$和正比例函数$y=kx$来解释函数图象的平移。
【答案】:
(1) 解:
由题意,函数$y=kx+b$经过点$(2,-1)$和$(-1,5)$,代入得:
$\begin{cases}2k + b = -1, \\-k + b = 5.\end{cases}$
解这个方程组,我们得到:
$\begin{cases}k = -2, \\b = 3.\end{cases}$
(2) 解:
由(1)我们知道,一次函数的解析式为$y=-2x+3$。
为了画出该函数的图象,我们需要找到它与坐标轴的交点。
当$x=0$时,$y=3$,得到交点$(0,3)$;
当$y=0$时,$x=\frac{3}{2}$,得到交点$\left(\frac{3}{2},0\right)$。
连接这两个点,我们得到一次函数的图象。
又因为一次函数$y=-2x+3$可以看作是正比例函数$y=-2x$向上平移$3$个单位得到的,所以函数图象可由正比例函数$y=-2x$的图象向上平移$3$个单位得到。
图略。
本题主要考查一次函数的性质,包括求解一次函数的表达式以及函数图象的平移。
(1) 对于求$k$和$b$的值,我们可以将给定的两个点$(2,-1)$和$(-1,5)$代入一次函数$y=kx+b$,得到两个方程,然后解这个方程组来找到$k$和$b$的值。
(2) 对于画出函数图象,我们需要先找到函数与坐标轴的交点,然后连接这些点来绘制函数图象。接着,我们可以通过比较一次函数$y=kx+b$和正比例函数$y=kx$来解释函数图象的平移。
【答案】:
(1) 解:
由题意,函数$y=kx+b$经过点$(2,-1)$和$(-1,5)$,代入得:
$\begin{cases}2k + b = -1, \\-k + b = 5.\end{cases}$
解这个方程组,我们得到:
$\begin{cases}k = -2, \\b = 3.\end{cases}$
(2) 解:
由(1)我们知道,一次函数的解析式为$y=-2x+3$。
为了画出该函数的图象,我们需要找到它与坐标轴的交点。
当$x=0$时,$y=3$,得到交点$(0,3)$;
当$y=0$时,$x=\frac{3}{2}$,得到交点$\left(\frac{3}{2},0\right)$。
连接这两个点,我们得到一次函数的图象。
又因为一次函数$y=-2x+3$可以看作是正比例函数$y=-2x$向上平移$3$个单位得到的,所以函数图象可由正比例函数$y=-2x$的图象向上平移$3$个单位得到。
图略。
6. 一次函数$y= -2x+3$的图象与坐标轴围成的三角形的面积为
$\frac{9}{4}$
.答案:解:当$x=0$时,$y=-2×0 + 3=3$,则函数与$y$轴交点坐标为$(0,3)$;
当$y=0$时,$-2x + 3=0$,解得$x=\frac{3}{2}$,则函数与$x$轴交点坐标为$(\frac{3}{2},0)$。
所以与坐标轴围成的三角形两直角边的长分别为$3$和$\frac{3}{2}$。
面积$S=\frac{1}{2}×3×\frac{3}{2}=\frac{9}{4}$。
$\frac{9}{4}$
当$y=0$时,$-2x + 3=0$,解得$x=\frac{3}{2}$,则函数与$x$轴交点坐标为$(\frac{3}{2},0)$。
所以与坐标轴围成的三角形两直角边的长分别为$3$和$\frac{3}{2}$。
面积$S=\frac{1}{2}×3×\frac{3}{2}=\frac{9}{4}$。
$\frac{9}{4}$
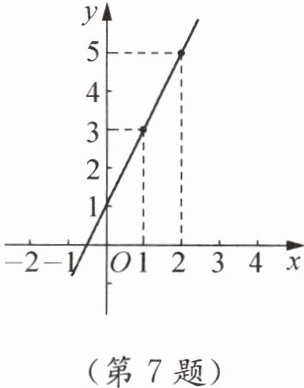
7. 小明说,在一次函数$y= kx+b$中,$x$每增加1,$kx增加了k$,$b$没变,因此$y也增加了k$,在如图所示的一次函数图象中,$x$从1变成2时,函数值从3变为5,增加了2,因此该一次函数中$k$的值是2.小明确定$k$的这种方法有道理吗?说说你的认识.
已知一次函数的图象经过$(-1,1)$,$(0,-1)$两点,用两种不同的方法求这个一次函数的表达式.
已知一次函数的图象经过$(-1,1)$,$(0,-1)$两点,用两种不同的方法求这个一次函数的表达式.

答案:【解析】:
本题主要考查一次函数的性质及表达式求解。
首先,分析小明的观点:
小明认为在一次函数$y = kx + b$中,当$x$每增加1时,$y$的增加量就是$k$。
这是正确的,因为当$x$变为$x+1$时,新的$y$值为$k(x+1) + b = kx + k + b$,与原$y$值$kx + b$相比,增加了$k$。
接着,利用给定的两点$(-1,1)$和$(0,-1)$来求一次函数的表达式:
方法一:利用斜率公式求$k$,
已知两点$(-1,1)$和$(0,-1)$,斜率$k$为:
$k = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-1 - 1}{0 - (-1)} = \frac{-2}{1} = -2$,
然后,利用点斜式$y - y_1 = k(x - x_1)$,选择点$(-1,1)$,得到:
$y - 1 = -2(x + 1)$,
整理得:$y = -2x - 1$。
方法二:利用待定系数法求$k$和$b$,
设一次函数为$y = kx + b$,将点$(-1,1)$和$(0,-1)$代入得:
$\begin{cases}-k + b = 1, \\b = -1.\end{cases}$
解这个方程组,已经知道$b = -1$,代入第一个方程得:
$-k - 1 = 1 \Rightarrow k = -2$,
所以,一次函数的表达式为$y = -2x - 1$。
综上所述,小明确定$k$的方法有道理,且这个一次函数的表达式为$y = -2x - 1$。
【答案】:
小明确定$k$的方法有道理;这个一次函数的表达式为$y = -2x - 1$。
本题主要考查一次函数的性质及表达式求解。
首先,分析小明的观点:
小明认为在一次函数$y = kx + b$中,当$x$每增加1时,$y$的增加量就是$k$。
这是正确的,因为当$x$变为$x+1$时,新的$y$值为$k(x+1) + b = kx + k + b$,与原$y$值$kx + b$相比,增加了$k$。
接着,利用给定的两点$(-1,1)$和$(0,-1)$来求一次函数的表达式:
方法一:利用斜率公式求$k$,
已知两点$(-1,1)$和$(0,-1)$,斜率$k$为:
$k = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-1 - 1}{0 - (-1)} = \frac{-2}{1} = -2$,
然后,利用点斜式$y - y_1 = k(x - x_1)$,选择点$(-1,1)$,得到:
$y - 1 = -2(x + 1)$,
整理得:$y = -2x - 1$。
方法二:利用待定系数法求$k$和$b$,
设一次函数为$y = kx + b$,将点$(-1,1)$和$(0,-1)$代入得:
$\begin{cases}-k + b = 1, \\b = -1.\end{cases}$
解这个方程组,已经知道$b = -1$,代入第一个方程得:
$-k - 1 = 1 \Rightarrow k = -2$,
所以,一次函数的表达式为$y = -2x - 1$。
综上所述,小明确定$k$的方法有道理,且这个一次函数的表达式为$y = -2x - 1$。
【答案】:
小明确定$k$的方法有道理;这个一次函数的表达式为$y = -2x - 1$。