一次函数 $ y = kx + b $ 中,$ k $,$ b $ 的符号和其图象的特征有什么关系?
(1) 观察下列函数:① $ y = 5 - 2x $;② $ y = -x + 3 $;③ $ y = x $;④ $ y = \frac{3}{2}x - 2 $;⑤ $ y = 5x - 6 $;⑥ $ y = -2x $. 其中,$ y $ 随 $ x $ 的增大而增大的有______,$ y $ 随 $ x $ 的增大而减小的有______,图象经过原点的有______,图象相互平行的是______(填序号).
(1) 观察下列函数:① $ y = 5 - 2x $;② $ y = -x + 3 $;③ $ y = x $;④ $ y = \frac{3}{2}x - 2 $;⑤ $ y = 5x - 6 $;⑥ $ y = -2x $. 其中,$ y $ 随 $ x $ 的增大而增大的有______,$ y $ 随 $ x $ 的增大而减小的有______,图象经过原点的有______,图象相互平行的是______(填序号).
答案:解:
(1) $y$ 随 $x$ 的增大而增大的有③④⑤,
$y$ 随 $x$ 的增大而减小的有①②⑥,
图象经过原点的有③⑥,
图象相互平行的是①⑥。
(1) $y$ 随 $x$ 的增大而增大的有③④⑤,
$y$ 随 $x$ 的增大而减小的有①②⑥,
图象经过原点的有③⑥,
图象相互平行的是①⑥。
例 在同一平面直角坐标系中,画出函数 $ y = x + 1 $,$ y = x - 1 $,$ y = -x + 1 $,$ y = -x - 1 $ 的图象. 观察图象,你发现了什么?
答案:【解析】:
本题主要考查了一次函数的图象绘制以及一次函数的性质。
首先,需要分别画出四个一次函数的图象。
对于 $y = x + 1$,这是一条斜率为1,截距为1的直线。
对于 $y = x - 1$,这是一条斜率为1,截距为-1的直线。
对于 $y = -x + 1$,这是一条斜率为-1,截距为1的直线。
对于 $y = -x - 1$,这是一条斜率为-1,截距为-1的直线。
在平面直角坐标系中,可以分别取两个点来确定每一条直线,然后连接这两点即可画出直线。
例如,对于 $y = x + 1$,可以取点 $(0,1)$ 和 $(1,2)$,然后连接这两点。
画出图象后,观察这四条直线,可以发现:
两条斜率为正的直线 $y = x + 1$ 和 $y = x - 1$ 是平行的,因为它们的斜率相同。
两条斜率为负的直线 $y = -x + 1$ 和 $y = -x - 1$ 也是平行的,因为它们的斜率相同。
斜率为正的直线与斜率为负的直线是垂直的,因为它们的斜率互为相反数的倒数。
【答案】:
图略。
通过观察图象,发现:
$y = x + 1$ 与 $y = x - 1$ 平行;
$y = -x + 1$ 与 $y = -x - 1$ 平行;
$y = x + 1$(或 $y = x - 1$)与 $y = -x + 1$(或 $y = -x - 1$)垂直。
本题主要考查了一次函数的图象绘制以及一次函数的性质。
首先,需要分别画出四个一次函数的图象。
对于 $y = x + 1$,这是一条斜率为1,截距为1的直线。
对于 $y = x - 1$,这是一条斜率为1,截距为-1的直线。
对于 $y = -x + 1$,这是一条斜率为-1,截距为1的直线。
对于 $y = -x - 1$,这是一条斜率为-1,截距为-1的直线。
在平面直角坐标系中,可以分别取两个点来确定每一条直线,然后连接这两点即可画出直线。
例如,对于 $y = x + 1$,可以取点 $(0,1)$ 和 $(1,2)$,然后连接这两点。
画出图象后,观察这四条直线,可以发现:
两条斜率为正的直线 $y = x + 1$ 和 $y = x - 1$ 是平行的,因为它们的斜率相同。
两条斜率为负的直线 $y = -x + 1$ 和 $y = -x - 1$ 也是平行的,因为它们的斜率相同。
斜率为正的直线与斜率为负的直线是垂直的,因为它们的斜率互为相反数的倒数。
【答案】:
图略。
通过观察图象,发现:
$y = x + 1$ 与 $y = x - 1$ 平行;
$y = -x + 1$ 与 $y = -x - 1$ 平行;
$y = x + 1$(或 $y = x - 1$)与 $y = -x + 1$(或 $y = -x - 1$)垂直。
1. 填空题:
(1)有下列函数:① $ y = 5 - 2x $;② $ y = -x + 3 $;③ $ y = x $;④ $ y = \frac{3}{2}x - 2 $;⑤ $ y = 5x - 6 $;⑥ $ y = -2x $. 其中,$ y $ 随 $ x $ 的增大而增大的有
(2)一次函数 $ y = -2x + 4 $ 的图象经过
(1)有下列函数:① $ y = 5 - 2x $;② $ y = -x + 3 $;③ $ y = x $;④ $ y = \frac{3}{2}x - 2 $;⑤ $ y = 5x - 6 $;⑥ $ y = -2x $. 其中,$ y $ 随 $ x $ 的增大而增大的有
③④⑤
,$ y $ 随 $ x $ 的增大而减小的有①②⑥
,图象经过原点的有③⑥
,图象相互平行的是①⑥
(填序号).(2)一次函数 $ y = -2x + 4 $ 的图象经过
一、二、四
象限,它与两坐标轴围成的三角形面积为4
.答案:(1)③④⑤;①②⑥;③⑥;①⑥
(2)一、二、四;4
(2)一、二、四;4
2. 选择题:
(1)在同一平面直角坐标系中有下列函数的图象:① $ y = -2x - 1 $;② $ y = 2x - 1 $;③ $ y = -2x $;④ $ y = -3x + 5 $;⑤ $ y = x - 1 $. 下列说法中,正确的是(
A. ①③的图象都过点 $ (0, -1) $
B. ①②③的图象相互平行
C. 将③的图象向下平移1个单位长度得到①的图象
D. ③④⑤的图象都过点 $ (1, 0) $
(2)已知一次函数 $ y = kx + b $ 的图象如图所示,则 $ k $,$ b $ 的取值范围是(
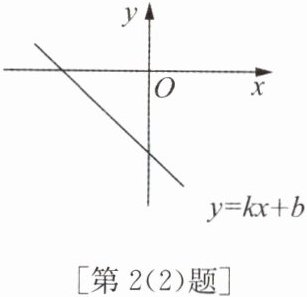
A. $ k > 0 $,$ b > 0 $
B. $ k > 0 $,$ b < 0 $
C. $ k < 0 $,$ b > 0 $
D. $ k < 0 $,$ b < 0 $
(1)在同一平面直角坐标系中有下列函数的图象:① $ y = -2x - 1 $;② $ y = 2x - 1 $;③ $ y = -2x $;④ $ y = -3x + 5 $;⑤ $ y = x - 1 $. 下列说法中,正确的是(
C
).A. ①③的图象都过点 $ (0, -1) $
B. ①②③的图象相互平行
C. 将③的图象向下平移1个单位长度得到①的图象
D. ③④⑤的图象都过点 $ (1, 0) $
(2)已知一次函数 $ y = kx + b $ 的图象如图所示,则 $ k $,$ b $ 的取值范围是(
D
).
A. $ k > 0 $,$ b > 0 $
B. $ k > 0 $,$ b < 0 $
C. $ k < 0 $,$ b > 0 $
D. $ k < 0 $,$ b < 0 $
答案:(1)
解:A. ①$y=-2x-1$,当$x=0$时,$y=-1$,过点$(0,-1)$;③$y=-2x$,当$x=0$时,$y=0$,过点$(0,0)$,A错误。
B. ①$k=-2$,②$k=2$,③$k=-2$,①③平行,②与①③不平行,B错误。
C. ③$y=-2x$向下平移1个单位得$y=-2x-1$,即①,C正确。
D. ③$y=-2x$,当$x=1$时,$y=-2\neq0$;④$y=-3x+5$,当$x=1$时,$y=2\neq0$;⑤$y=x-1$,当$x=1$时,$y=0$,D错误。
答案:C
(2)
解:由图知,函数$y=kx+b$的图象从左到右下降,$k<0$;与$y$轴交于负半轴,$b<0$。
答案:D
解:A. ①$y=-2x-1$,当$x=0$时,$y=-1$,过点$(0,-1)$;③$y=-2x$,当$x=0$时,$y=0$,过点$(0,0)$,A错误。
B. ①$k=-2$,②$k=2$,③$k=-2$,①③平行,②与①③不平行,B错误。
C. ③$y=-2x$向下平移1个单位得$y=-2x-1$,即①,C正确。
D. ③$y=-2x$,当$x=1$时,$y=-2\neq0$;④$y=-3x+5$,当$x=1$时,$y=2\neq0$;⑤$y=x-1$,当$x=1$时,$y=0$,D错误。
答案:C
(2)
解:由图知,函数$y=kx+b$的图象从左到右下降,$k<0$;与$y$轴交于负半轴,$b<0$。
答案:D