例1 已知关于x的一次函数$y= (2k-1)x+(2k+1)$.
(1)当k满足什么条件时,函数值y随x的增大而增大？
(2)当k取何值时,$y= (2k-1)x+(2k+1)$的图象经过原点？
(3)当k满足什么条件时,函数$y= (2k-1)x+(2k+1)$的图象与y轴的交点在x轴的上方？

(1)小明在平路上的骑车速度为km/h,他途中休息了h；
(2)求线段AB,BC相应的函数表达式；
设线段AB的函数表达式为$y = kx + b$，将$A(0.3, 4.5)$，$B(0.5, 6.5)$代入，得$\begin{cases}0.3k + b = 4.5 \\ 0.5k + b = 6.5\end{cases}$，解得$\begin{cases}k = 10 \\ b = 1.5\end{cases}$，所以线段AB的函数表达式为$y = 10x + 1.5(0.3 \leq x \leq 0.5)$。
设线段BC的函数表达式为$y = mx + n$，将$B(0.5, 6.5)$，$C(0.6, 4.5)$代入，得$\begin{cases}0.5m + n = 6.5 \\ 0.6m + n = 4.5\end{cases}$，解得$\begin{cases}m = -20 \\ n = 16.5\end{cases}$，所以线段BC的函数表达式为$y = -20x + 16.5(0.5 \leq x \leq 0.6)$。
(3)如果小明两次经过途中某一地点的时间间隔为0.15 h,那么该地点距离甲地多远？
设该地点距离甲地$a$km。
当$0 \leq x \leq 0.3$时，$y = 15x$，则$x = \frac{a}{15}$。
当$0.6 \leq x \leq 1$时，设$y = px + q$，将$C(0.6, 4.5)$，$E(1, 0)$代入，得$\begin{cases}0.6p + q = 4.5 \\ p + q = 0\end{cases}$，解得$\begin{cases}p = -11.25 \\ q = 11.25\end{cases}$，所以$y = -11.25x + 11.25$，则$x = \frac{11.25 - a}{11.25}$。
由题意得$\frac{11.25 - a}{11.25} - \frac{a}{15} = 0.15$，解得$a = 4.5$。
当$0.3 \leq x \leq 0.5$时，$y = 10x + 1.5$，则$x = \frac{a - 1.5}{10}$。
当$0.6 \leq x \leq 1$时，$x = \frac{11.25 - a}{11.25}$，由题意得$\frac{11.25 - a}{11.25} - \frac{a - 1.5}{10} = 0.15$，解得$a = 4.5$。
综上，该地点距离甲地$4.5$km。

1. 填空题：
(1)在函数$y= \frac{2}{x-1}$中,自变量x的取值范围是.
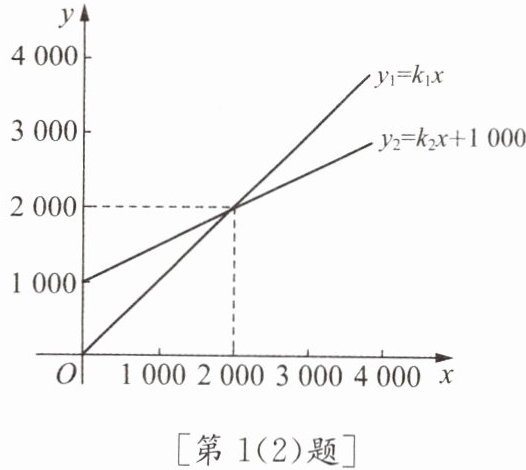
(2)一次函数$y_{1}= k_{1}x和y_{2}= k_{2}x+1000$的图象如图所示,当x时,$y_{1}＞y_{2}$.

(3)将函数$y= 2x+3$的图象平移,使它经过点$(2,-1)$,平移后图象对应的函数表达式是.
(4)在函数$y= x+4$中,若自变量x的取值范围是$-3＜x＜-1$,则函数值y的取值范围为.
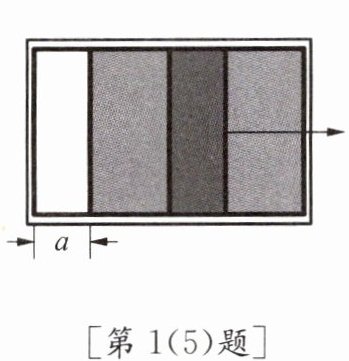
(5)如图,一扇长方形推拉窗的高为1.5 m,活动窗户的通风面积$S m^{2}$关于拉开长度a m的函数表达式是.

(6)祖孙两人进行爬山比赛,孙子让爷爷先行,然后追赶爷爷,图中两条线段分别表示祖孙两人离开山脚的距离y m与比赛时间t min之间的关系,孙子让爷爷先行了m,两个人的速度分别为,山脚距山顶m.
]