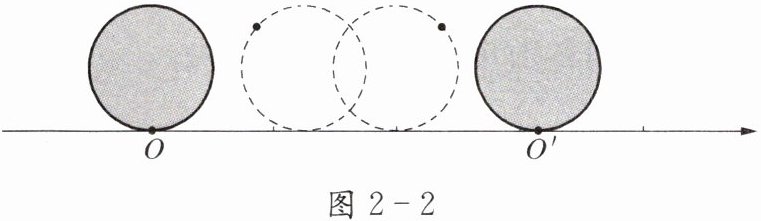
如图2-2,半径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O'.点O'所表示的是什么数?这个数是有理数吗?

答案:【解析】:
首先,我们知道圆的半径为1个单位长度。当圆从原点沿数轴向右滚动一周时,其滚动的距离等于圆的周长。
圆的周长公式为 $C = 2\pi r$,其中 $r$ 是圆的半径。
将 $r = 1$ 代入公式,得到圆的周长为 $2\pi × 1 = 2\pi$。
因此,当圆从原点滚动到点 $O'$ 时,点 $O'$ 所表示的数就是圆滚动的距离,即 $2\pi$。
接下来,我们需要判断 $2\pi$ 是否为有理数。
有理数是可以表示为两个整数之比的数,而 $\pi$ 是一个无理数,即不能表示为两个整数的比。
因此,$2\pi$ 也是无理数,因为它仍然包含 $\pi$ 这一无理数部分。
【答案】:
点 $O'$ 所表示的数是 $2\pi$,这个数是无理数。
首先,我们知道圆的半径为1个单位长度。当圆从原点沿数轴向右滚动一周时,其滚动的距离等于圆的周长。
圆的周长公式为 $C = 2\pi r$,其中 $r$ 是圆的半径。
将 $r = 1$ 代入公式,得到圆的周长为 $2\pi × 1 = 2\pi$。
因此,当圆从原点滚动到点 $O'$ 时,点 $O'$ 所表示的数就是圆滚动的距离,即 $2\pi$。
接下来,我们需要判断 $2\pi$ 是否为有理数。
有理数是可以表示为两个整数之比的数,而 $\pi$ 是一个无理数,即不能表示为两个整数的比。
因此,$2\pi$ 也是无理数,因为它仍然包含 $\pi$ 这一无理数部分。
【答案】:
点 $O'$ 所表示的数是 $2\pi$,这个数是无理数。
例1 下列各数中,哪些是有理数?哪些是无理数?哪些是实数?
$\sqrt{289}$,$\frac{1}{2}$,$\sqrt{5}$,$\frac{22}{7}$,0.2020020002…(每两个2之间0的个数逐次增加),$\sqrt[3]{-27}$,$\frac{\pi}{3}$,$-0.\dot{8}\dot{9}$,$\sqrt[3]{9}$.
$\sqrt{289}$,$\frac{1}{2}$,$\sqrt{5}$,$\frac{22}{7}$,0.2020020002…(每两个2之间0的个数逐次增加),$\sqrt[3]{-27}$,$\frac{\pi}{3}$,$-0.\dot{8}\dot{9}$,$\sqrt[3]{9}$.
答案:【解析】:
本题主要考察有理数、无理数和实数的定义及识别。
有理数:可以表示为两个整数的比的数,即分数形式。
无理数:不能表示为两个整数的比的数,例如某些平方根、立方根、π等。
实数:包括有理数和无理数的所有数。
根据这些定义,我们可以逐一判断给出的数:
$\sqrt{289}$:289的平方根是17,是整数,因此也是有理数。
$\frac{1}{2}$:是分数形式,因此是有理数。
$\sqrt{5}$:5的平方根不能表示为两个整数的比,因此是无理数。
$\frac{22}{7}$:是分数形式,因此是有理数。
$0.2020020002\ldots$(每两个2之间0的个数逐次增加):这是一个无限不循环小数,因此是无理数。
$\sqrt[3]{-27}$:-27的立方根是-3,是整数,因此也是有理数。
$\frac{\pi}{3}$:π是一个无理数,因此$\frac{\pi}{3}$也是无理数。
$-0.\dot{8}\dot{9}$:这是一个无限循环小数,因此是有理数。
$\sqrt[3]{9}$:9的立方根不能表示为两个整数的比,因此是无理数。
【答案】:
有理数:$\sqrt{289}$,$\frac{1}{2}$,$\frac{22}{7}$,$\sqrt[3]{-27}$,$-0.\dot{8}\dot{9}$。
无理数:$\sqrt{5}$,$0.2020020002\ldots$(每两个2之间0的个数逐次增加),$\frac{\pi}{3}$,$\sqrt[3]{9}$。
实数:所有列出的数都是实数。
本题主要考察有理数、无理数和实数的定义及识别。
有理数:可以表示为两个整数的比的数,即分数形式。
无理数:不能表示为两个整数的比的数,例如某些平方根、立方根、π等。
实数:包括有理数和无理数的所有数。
根据这些定义,我们可以逐一判断给出的数:
$\sqrt{289}$:289的平方根是17,是整数,因此也是有理数。
$\frac{1}{2}$:是分数形式,因此是有理数。
$\sqrt{5}$:5的平方根不能表示为两个整数的比,因此是无理数。
$\frac{22}{7}$:是分数形式,因此是有理数。
$0.2020020002\ldots$(每两个2之间0的个数逐次增加):这是一个无限不循环小数,因此是无理数。
$\sqrt[3]{-27}$:-27的立方根是-3,是整数,因此也是有理数。
$\frac{\pi}{3}$:π是一个无理数,因此$\frac{\pi}{3}$也是无理数。
$-0.\dot{8}\dot{9}$:这是一个无限循环小数,因此是有理数。
$\sqrt[3]{9}$:9的立方根不能表示为两个整数的比,因此是无理数。
【答案】:
有理数:$\sqrt{289}$,$\frac{1}{2}$,$\frac{22}{7}$,$\sqrt[3]{-27}$,$-0.\dot{8}\dot{9}$。
无理数:$\sqrt{5}$,$0.2020020002\ldots$(每两个2之间0的个数逐次增加),$\frac{\pi}{3}$,$\sqrt[3]{9}$。
实数:所有列出的数都是实数。
例2 判断$\frac{\sqrt{5}-1}{2}$与1的大小.
答案:【解析】:
本题要求我们判断两个数的大小,其中涉及到实数的运算和大小比较。由于$\frac{\sqrt{5}-1}{2}$是一个无理数与有理数的混合表达式,我们可以通过估算或者利用不等式性质来判断其与1的大小关系。考虑到$\sqrt{5}$的值大约等于2.236,是一个大于2但小于3的数,因此$\sqrt{5}-1$会是一个大于1但小于2的数,再除以2,其结果应当仍然小于1。为了更严谨的证明,我们也可以利用不等式性质进行比较。
【答案】:
解:
首先,我们计算$\frac{\sqrt{5}-1}{2} - 1$的值,
$\frac{\sqrt{5}-1}{2} - 1 = \frac{\sqrt{5}-1-2}{2} = \frac{\sqrt{5}-3}{2}$
由于$\sqrt{5} < 3$(因为$5 < 9$,所以$\sqrt{5} < \sqrt{9} = 3$),
所以$\frac{\sqrt{5}-3}{2} < 0$,
因此,$\frac{\sqrt{5}-1}{2} < 1$。
本题要求我们判断两个数的大小,其中涉及到实数的运算和大小比较。由于$\frac{\sqrt{5}-1}{2}$是一个无理数与有理数的混合表达式,我们可以通过估算或者利用不等式性质来判断其与1的大小关系。考虑到$\sqrt{5}$的值大约等于2.236,是一个大于2但小于3的数,因此$\sqrt{5}-1$会是一个大于1但小于2的数,再除以2,其结果应当仍然小于1。为了更严谨的证明,我们也可以利用不等式性质进行比较。
【答案】:
解:
首先,我们计算$\frac{\sqrt{5}-1}{2} - 1$的值,
$\frac{\sqrt{5}-1}{2} - 1 = \frac{\sqrt{5}-1-2}{2} = \frac{\sqrt{5}-3}{2}$
由于$\sqrt{5} < 3$(因为$5 < 9$,所以$\sqrt{5} < \sqrt{9} = 3$),
所以$\frac{\sqrt{5}-3}{2} < 0$,
因此,$\frac{\sqrt{5}-1}{2} < 1$。
1. 填空题:
(1)
(2)请写出4个无理数:
(1)
无限不循环小数
称为无理数.(2)请写出4个无理数:
$\sqrt{2}$,$\sqrt{3}$,$\pi$,$1.010010001\cdots$(每两个1之间依次多一个0)
.答案:(1)无限不循环小数
(2)$\sqrt{2}$,$\sqrt{3}$,$\pi$,$1.010010001\cdots$(每两个1之间依次多一个0)
(2)$\sqrt{2}$,$\sqrt{3}$,$\pi$,$1.010010001\cdots$(每两个1之间依次多一个0)