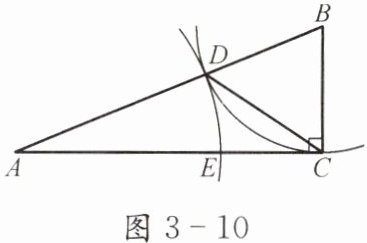
例1 如图3-10,在△ABC中,∠ACB= 90°,以点B为圆心,BC为半径画弧,交边AB于点D,以点A为圆心,AD为半径画弧,交边AC于点E,连接CD.
(1)已知∠A= 25°,求∠ACD的度数;
(2)已知BC= 2.5,CE= 2,求AD的长.
(1)已知∠A= 25°,求∠ACD的度数;
(2)已知BC= 2.5,CE= 2,求AD的长.

答案:【解析】:本题主要考查了直角三角形的性质以及等腰三角形的性质,利用这些性质来求解相关角度和边长。
(1)在$\triangle ABC$中,已知$\angle ACB = 90^{\circ}$,$\angle A = 25^{\circ}$,根据直角三角形两锐角互余,可求出$\angle B$的度数,再结合$BC = BD$(以点$B$为圆心,$BC$为半径画弧交$AB$于点$D$),利用等腰三角形两底角相等的性质求出$\angle BCD$,最后用$\angle ACB$减去$\angle BCD$得到$\angle ACD$的度数。
(2)由(1)可知$BC = BD = 2.5$,$AD = AE$(以点$A$为圆心,$AD$为半径画弧交$AC$于点$E$),设$AD = x$,则$AE = x$,$AC = AE + CE = x + 2$,在$Rt\triangle ABC$中,根据勾股定理列出关于$x$的方程,进而求出$AD$的长。
【答案】:解:(1)在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 25^{\circ}$,
根据直角三角形两锐角互余,可得$\angle B = 90^{\circ} - \angle A = 90^{\circ} - 25^{\circ} = 65^{\circ}$。
因为$BC = BD$,所以$\triangle BCD$是等腰三角形,
根据等腰三角形两底角相等,可得$\angle BCD = \angle BDC$。
在$\triangle BCD$中,$\angle BCD = \frac{1}{2}×(180^{\circ} - \angle B) = \frac{1}{2}×(180^{\circ} - 65^{\circ}) = 57.5^{\circ}$。
所以$\angle ACD = \angle ACB - \angle BCD = 90^{\circ} - 57.5^{\circ} = 32.5^{\circ}$。
(2)由(1)知$BC = BD = 2.5$,设$AD = x$,因为$AD = AE$,所以$AE = x$。
又因为$CE = 2$,所以$AC = AE + CE = x + 2$。
在$Rt\triangle ABC$中,根据勾股定理$AB^{2} = AC^{2} + BC^{2}$,
$AB = AD + BD = x + 2.5$,$BC = 2.5$,$AC = x + 2$,
则$(x + 2.5)^{2} = (x + 2)^{2} + 2.5^{2}$。
展开式子得$x^{2} + 5x + 6.25 = x^{2} + 4x + 4 + 6.25$,
移项可得$x^{2} + 5x - x^{2} - 4x = 4 + 6.25 - 6.25$,
合并同类项得$x = 4$。
所以$AD$的长为$4$。
(1)在$\triangle ABC$中,已知$\angle ACB = 90^{\circ}$,$\angle A = 25^{\circ}$,根据直角三角形两锐角互余,可求出$\angle B$的度数,再结合$BC = BD$(以点$B$为圆心,$BC$为半径画弧交$AB$于点$D$),利用等腰三角形两底角相等的性质求出$\angle BCD$,最后用$\angle ACB$减去$\angle BCD$得到$\angle ACD$的度数。
(2)由(1)可知$BC = BD = 2.5$,$AD = AE$(以点$A$为圆心,$AD$为半径画弧交$AC$于点$E$),设$AD = x$,则$AE = x$,$AC = AE + CE = x + 2$,在$Rt\triangle ABC$中,根据勾股定理列出关于$x$的方程,进而求出$AD$的长。
【答案】:解:(1)在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 25^{\circ}$,
根据直角三角形两锐角互余,可得$\angle B = 90^{\circ} - \angle A = 90^{\circ} - 25^{\circ} = 65^{\circ}$。
因为$BC = BD$,所以$\triangle BCD$是等腰三角形,
根据等腰三角形两底角相等,可得$\angle BCD = \angle BDC$。
在$\triangle BCD$中,$\angle BCD = \frac{1}{2}×(180^{\circ} - \angle B) = \frac{1}{2}×(180^{\circ} - 65^{\circ}) = 57.5^{\circ}$。
所以$\angle ACD = \angle ACB - \angle BCD = 90^{\circ} - 57.5^{\circ} = 32.5^{\circ}$。
(2)由(1)知$BC = BD = 2.5$,设$AD = x$,因为$AD = AE$,所以$AE = x$。
又因为$CE = 2$,所以$AC = AE + CE = x + 2$。
在$Rt\triangle ABC$中,根据勾股定理$AB^{2} = AC^{2} + BC^{2}$,
$AB = AD + BD = x + 2.5$,$BC = 2.5$,$AC = x + 2$,
则$(x + 2.5)^{2} = (x + 2)^{2} + 2.5^{2}$。
展开式子得$x^{2} + 5x + 6.25 = x^{2} + 4x + 4 + 6.25$,
移项可得$x^{2} + 5x - x^{2} - 4x = 4 + 6.25 - 6.25$,
合并同类项得$x = 4$。
所以$AD$的长为$4$。
例2 如图3-11,△ACB和△ECD都是等腰直角三角形,∠ACB与∠ECD为直角,△ACB的顶点A在△ECD的斜边DE上.求证:$AE^{2}+AD^{2}= 2AC^{2}$.(提示:连接BD)


答案:【解析】:本题主要考查了等腰直角三角形的性质、全等三角形的判定与性质以及勾股定理的应用。
连接$BD$,由等腰直角三角形的性质可得$AC = BC$,$EC = CD$,$\angle ACB=\angle ECD = 90^{\circ}$,进而推出$\angle ACE=\angle BCD$,利用$SAS$证明$\triangle ACE\cong\triangle BCD$,得到$AE = BD$,$\angle E=\angle CDB$,再根据$\angle E+\angle EDC = 90^{\circ}$推出$\angle ADB = 90^{\circ}$,最后在$Rt\triangle ADB$中运用勾股定理得出结论。
【答案】:证明:
连接$BD$。
∵$\triangle ACB$与$\triangle ECD$都是等腰直角三角形,
∴$AC = BC$,$EC = CD$,$\angle ACB=\angle ECD = 90^{\circ}$。
∵$\angle ACB+\angle ACD=\angle ECD+\angle ACD$,
∴$\angle ACE=\angle BCD$。
在$\triangle ACE$和$\triangle BCD$中,
$\begin{cases}AC = BC\\\angle ACE=\angle BCD\\EC = CD\end{cases}$
∴$\triangle ACE\cong\triangle BCD(SAS)$。
∴$AE = BD$,$\angle E=\angle CDB$。
∵$\angle E+\angle EDC = 90^{\circ}$,
∴$\angle CDB+\angle EDC = 90^{\circ}$,即$\angle ADB = 90^{\circ}$。
在$Rt\triangle ADB$中,由勾股定理得$AD^{2}+BD^{2}=AB^{2}$。
又∵在等腰直角$\triangle ACB$中,$AB^{2}=AC^{2}+BC^{2}=2AC^{2}$,且$BD = AE$,
∴$AE^{2}+AD^{2}=2AC^{2}$。
连接$BD$,由等腰直角三角形的性质可得$AC = BC$,$EC = CD$,$\angle ACB=\angle ECD = 90^{\circ}$,进而推出$\angle ACE=\angle BCD$,利用$SAS$证明$\triangle ACE\cong\triangle BCD$,得到$AE = BD$,$\angle E=\angle CDB$,再根据$\angle E+\angle EDC = 90^{\circ}$推出$\angle ADB = 90^{\circ}$,最后在$Rt\triangle ADB$中运用勾股定理得出结论。
【答案】:证明:
连接$BD$。
∵$\triangle ACB$与$\triangle ECD$都是等腰直角三角形,
∴$AC = BC$,$EC = CD$,$\angle ACB=\angle ECD = 90^{\circ}$。
∵$\angle ACB+\angle ACD=\angle ECD+\angle ACD$,
∴$\angle ACE=\angle BCD$。
在$\triangle ACE$和$\triangle BCD$中,
$\begin{cases}AC = BC\\\angle ACE=\angle BCD\\EC = CD\end{cases}$
∴$\triangle ACE\cong\triangle BCD(SAS)$。
∴$AE = BD$,$\angle E=\angle CDB$。
∵$\angle E+\angle EDC = 90^{\circ}$,
∴$\angle CDB+\angle EDC = 90^{\circ}$,即$\angle ADB = 90^{\circ}$。
在$Rt\triangle ADB$中,由勾股定理得$AD^{2}+BD^{2}=AB^{2}$。
又∵在等腰直角$\triangle ACB$中,$AB^{2}=AC^{2}+BC^{2}=2AC^{2}$,且$BD = AE$,
∴$AE^{2}+AD^{2}=2AC^{2}$。
1. 已知甲、乙从同一地点出发,甲往东走了4 km,乙往南走了3 km,这时甲、乙相距
5
km.答案:【解析】:
本题考查勾股定理的应用。甲往东走了4km,乙往南走了3km,由于东和南方向垂直,因此甲、乙和出发点构成了一个直角三角形。其中,甲走的距离是直角三角形的一条直角边,长度为4km;乙走的距离也是直角三角形的一条直角边,长度为3km。要求甲、乙之间的距离,即求该直角三角形的斜边长度。
根据勾股定理,直角三角形的斜边$c$满足:
$c = \sqrt{a^2 + b^2}$
其中,$a$和$b$是直角三角形的两条直角边。
将$a=4$,$b=3$代入公式,得:
$c = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5(km)$
所以,甲、乙相距5km。
【答案】:
5
本题考查勾股定理的应用。甲往东走了4km,乙往南走了3km,由于东和南方向垂直,因此甲、乙和出发点构成了一个直角三角形。其中,甲走的距离是直角三角形的一条直角边,长度为4km;乙走的距离也是直角三角形的一条直角边,长度为3km。要求甲、乙之间的距离,即求该直角三角形的斜边长度。
根据勾股定理,直角三角形的斜边$c$满足:
$c = \sqrt{a^2 + b^2}$
其中,$a$和$b$是直角三角形的两条直角边。
将$a=4$,$b=3$代入公式,得:
$c = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5(km)$
所以,甲、乙相距5km。
【答案】:
5
2. 在△ABC中,AB= 20,AC= 15,边BC上的高为12,则△ABC的面积为______
150或42
.答案:解:情况一:高在△ABC内部
设BC边上的高为AD,AD=12
在Rt△ABD中,BD=√(AB²-AD²)=√(20²-12²)=16
在Rt△ACD中,CD=√(AC²-AD²)=√(15²-12²)=9
BC=BD+CD=16+9=25
S△ABC=1/2×BC×AD=1/2×25×12=150
情况二:高在△ABC外部
BC=BD-CD=16-9=7
S△ABC=1/2×BC×AD=1/2×7×12=42
150或42
设BC边上的高为AD,AD=12
在Rt△ABD中,BD=√(AB²-AD²)=√(20²-12²)=16
在Rt△ACD中,CD=√(AC²-AD²)=√(15²-12²)=9
BC=BD+CD=16+9=25
S△ABC=1/2×BC×AD=1/2×25×12=150
情况二:高在△ABC外部
BC=BD-CD=16-9=7
S△ABC=1/2×BC×AD=1/2×7×12=42
150或42
3. 如图,两个阴影部分都是正方形,两个正方形的面积之比为1:2,则这两个正方形的面积分别是__
16,32
__.答案:【解析】:
本题可先根据勾股定理求出直角三角形另一条直角边的平方,再结合两个正方形面积之比求出两个正方形的面积。
步骤一:根据勾股定理求出直角三角形另一条直角边的平方
在直角三角形中,两条直角边的平方和等于斜边的平方。
已知该直角三角形的斜边长为$10$,一条直角边长为$8$,设另一条直角边长为$a$,根据勾股定理可得$a^{2}+8^{2}=10^{2}$,即$a^{2}=10^{2}-8^{2}=100 - 64 = 36$。
因为两个阴影部分都是正方形,正方形的面积等于边长的平方,所以两个正方形的面积分别为$a^{2}$和$8^{2}$,即$36$和$64$。
步骤二:根据两个正方形面积之比进行验证
已知两个正方形的面积之比为$1:2$,而$36:64 = 9:16$不符合要求,说明我们设的另一条直角边对应的正方形面积不是较小的那个。
因为两个正方形面积之比为$1:2$,设较小的正方形面积为$x$,则较大的正方形面积为$2x$,且$x + 2x = 36 + 64$(两个正方形面积之和等于直角三角形两条直角边平方和),即$3x = 100$,$x=\frac{100}{3}$不符合题意。
我们重新分析,设较小的正方形面积为$S_1$,较大的正方形面积为$S_2$,由面积比$\frac{S_1}{S_2}=\frac{1}{2}$,即$S_2 = 2S_1$,且$S_1+S_2=8^{2}+$(另一条直角边的平方)。
因为$8^{2}=64$,设$S_1 = k$,则$S_2 = 2k$,$k + 2k=64+$(另一条直角边的平方),又因为直角三角形另一条直角边的平方$ = 10^{2}-8^{2}=36$,所以$3k=64 + 36-64$(这里$64$是已知直角边对应正方形面积,$36$是求出的另一条直角边平方),$3k = 36$,解得$k = 16$,则$S_2 = 2k = 32$。
【答案】:$16$,$32$
本题可先根据勾股定理求出直角三角形另一条直角边的平方,再结合两个正方形面积之比求出两个正方形的面积。
步骤一:根据勾股定理求出直角三角形另一条直角边的平方
在直角三角形中,两条直角边的平方和等于斜边的平方。
已知该直角三角形的斜边长为$10$,一条直角边长为$8$,设另一条直角边长为$a$,根据勾股定理可得$a^{2}+8^{2}=10^{2}$,即$a^{2}=10^{2}-8^{2}=100 - 64 = 36$。
因为两个阴影部分都是正方形,正方形的面积等于边长的平方,所以两个正方形的面积分别为$a^{2}$和$8^{2}$,即$36$和$64$。
步骤二:根据两个正方形面积之比进行验证
已知两个正方形的面积之比为$1:2$,而$36:64 = 9:16$不符合要求,说明我们设的另一条直角边对应的正方形面积不是较小的那个。
因为两个正方形面积之比为$1:2$,设较小的正方形面积为$x$,则较大的正方形面积为$2x$,且$x + 2x = 36 + 64$(两个正方形面积之和等于直角三角形两条直角边平方和),即$3x = 100$,$x=\frac{100}{3}$不符合题意。
我们重新分析,设较小的正方形面积为$S_1$,较大的正方形面积为$S_2$,由面积比$\frac{S_1}{S_2}=\frac{1}{2}$,即$S_2 = 2S_1$,且$S_1+S_2=8^{2}+$(另一条直角边的平方)。
因为$8^{2}=64$,设$S_1 = k$,则$S_2 = 2k$,$k + 2k=64+$(另一条直角边的平方),又因为直角三角形另一条直角边的平方$ = 10^{2}-8^{2}=36$,所以$3k=64 + 36-64$(这里$64$是已知直角边对应正方形面积,$36$是求出的另一条直角边平方),$3k = 36$,解得$k = 16$,则$S_2 = 2k = 32$。
【答案】:$16$,$32$
4. 如图,BC= 1,AB= 2,AF= 3,则正方形CDEF的边长为______.


√7
答案:解:设正方形CDEF的边长为x。
在Rt△ABC中,∠B=90°,AB=2,BC=1,
由勾股定理得AC²=AB²+BC²=2²+1²=5。
在Rt△ACF中,∠A=90°,AF=3,AC²=5,
由勾股定理得CF²=AF²+AC²=3²+5=14。
在Rt△CFE中,∠F=90°,CF²=14,EF=CF=x,
由勾股定理得CF²=EF²+CE²,即14=x²+x²,
解得x=√7(负值舍去)。
√7
在Rt△ABC中,∠B=90°,AB=2,BC=1,
由勾股定理得AC²=AB²+BC²=2²+1²=5。
在Rt△ACF中,∠A=90°,AF=3,AC²=5,
由勾股定理得CF²=AF²+AC²=3²+5=14。
在Rt△CFE中,∠F=90°,CF²=14,EF=CF=x,
由勾股定理得CF²=EF²+CE²,即14=x²+x²,
解得x=√7(负值舍去)。
√7