4. 如图,在四边形ABCD中,各个顶点的坐标分别是(-2,8),(-11,6),(-14,0),(0,0).
(1)求四边形ABCD的面积.
(2)如果各个顶点的纵坐标保持不变,横坐标增加2,所得的四边形面积是多少?
(3)你有什么发现?
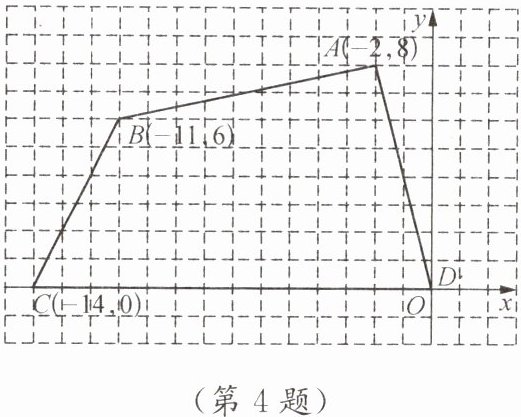
(1)求四边形ABCD的面积.
(2)如果各个顶点的纵坐标保持不变,横坐标增加2,所得的四边形面积是多少?
(3)你有什么发现?

答案:(1)解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F。
∵A(-2,8),B(-11,6),C(-14,0),D(0,0),
∴AE=8,OE=2,BF=6,OF=11,OD=0,OC=14,
∴CD=14,DE=OE=2,EF=OF-OE=11-2=9,FC=OC-OF=14-11=3。
S四边形ABCD=S△BCF+S梯形ABFE+S△AED
=1/2×FC×BF+1/2×(BF+AE)×EF+1/2×DE×AE
=1/2×3×6+1/2×(6+8)×9+1/2×2×8
=9+63+8=80。
(2)解:80。
(3)解:图形平移后,面积不变。
∵A(-2,8),B(-11,6),C(-14,0),D(0,0),
∴AE=8,OE=2,BF=6,OF=11,OD=0,OC=14,
∴CD=14,DE=OE=2,EF=OF-OE=11-2=9,FC=OC-OF=14-11=3。
S四边形ABCD=S△BCF+S梯形ABFE+S△AED
=1/2×FC×BF+1/2×(BF+AE)×EF+1/2×DE×AE
=1/2×3×6+1/2×(6+8)×9+1/2×2×8
=9+63+8=80。
(2)解:80。
(3)解:图形平移后,面积不变。
5. 在平面直角坐标系中,对于点P(a,b)和Q(c,d),给出如下的定义:点P(a,b),Q(c,d)的横坐标差的绝对值和它们的纵坐标差的绝对值中较小的一个(若它们相等,则取其中任意一个)称为P,Q两点的"近距",记为d(P,Q).即:若|a-c|≤|b-d|,则d(P,Q)= |a-c|;若|a-c|>|b-d|,则d(P,Q)= |b-d|.
(1)请你直接写出A(-3,0),B(-1,4)的"近距"d(A,B)= ______
(2)在条件(1)下,将线段AB向右平移4个单位长度至线段CD,其中点A,B分别对应点C,D.若在坐标轴上存在点E,使d(D,E)= √2,请求出点E的坐标.

解:由题意得,点B(-1,4)向右平移4个单位长度得到点D,D点坐标为(3,4)。
当点E在x轴上时,设E(m,0)。
若|m-3|≤|0-4|=4,则d(D,E)=|m-3|=√2,解得m=3+√2或m=3-√2,点E坐标为(3+√2,0)或(3-√2,0);
若|m-3|>4,则d(D,E)=4≠√2,无解。
当点E在y轴上时,设E(0,n)。
若|0-3|=3≤|n-4|,则d(D,E)=3≠√2,无解;
若|0-3|>|n-4|,则d(D,E)=|n-4|=√2,解得n=4+√2或n=4-√2,点E坐标为(0,4+√2)或(0,4-√2)。
综上,点E的坐标为(3+√2,0)、(3-√2,0)、(0,4+√2)、(0,4-√2)。
(1)请你直接写出A(-3,0),B(-1,4)的"近距"d(A,B)= ______
2
.(2)在条件(1)下,将线段AB向右平移4个单位长度至线段CD,其中点A,B分别对应点C,D.若在坐标轴上存在点E,使d(D,E)= √2,请求出点E的坐标.

解:由题意得,点B(-1,4)向右平移4个单位长度得到点D,D点坐标为(3,4)。
当点E在x轴上时,设E(m,0)。
若|m-3|≤|0-4|=4,则d(D,E)=|m-3|=√2,解得m=3+√2或m=3-√2,点E坐标为(3+√2,0)或(3-√2,0);
若|m-3|>4,则d(D,E)=4≠√2,无解。
当点E在y轴上时,设E(0,n)。
若|0-3|=3≤|n-4|,则d(D,E)=3≠√2,无解;
若|0-3|>|n-4|,则d(D,E)=|n-4|=√2,解得n=4+√2或n=4-√2,点E坐标为(0,4+√2)或(0,4-√2)。
综上,点E的坐标为(3+√2,0)、(3-√2,0)、(0,4+√2)、(0,4-√2)。
答案:(1) 2
(2) 解:由题意得,点B(-1,4)向右平移4个单位长度得到点D,D点坐标为(3,4)。
当点E在x轴上时,设E(m,0)。
若|m-3|≤|0-4|=4,则d(D,E)=|m-3|=√2,解得m=3+√2或m=3-√2,点E坐标为(3+√2,0)或(3-√2,0);
若|m-3|>4,则d(D,E)=4≠√2,无解。
当点E在y轴上时,设E(0,n)。
若|0-3|=3≤|n-4|,则d(D,E)=3≠√2,无解;
若|0-3|>|n-4|,则d(D,E)=|n-4|=√2,解得n=4+√2或n=4-√2,点E坐标为(0,4+√2)或(0,4-√2)。
综上,点E的坐标为(3+√2,0)、(3-√2,0)、(0,4+√2)、(0,4-√2)。
(2) 解:由题意得,点B(-1,4)向右平移4个单位长度得到点D,D点坐标为(3,4)。
当点E在x轴上时,设E(m,0)。
若|m-3|≤|0-4|=4,则d(D,E)=|m-3|=√2,解得m=3+√2或m=3-√2,点E坐标为(3+√2,0)或(3-√2,0);
若|m-3|>4,则d(D,E)=4≠√2,无解。
当点E在y轴上时,设E(0,n)。
若|0-3|=3≤|n-4|,则d(D,E)=3≠√2,无解;
若|0-3|>|n-4|,则d(D,E)=|n-4|=√2,解得n=4+√2或n=4-√2,点E坐标为(0,4+√2)或(0,4-√2)。
综上,点E的坐标为(3+√2,0)、(3-√2,0)、(0,4+√2)、(0,4-√2)。