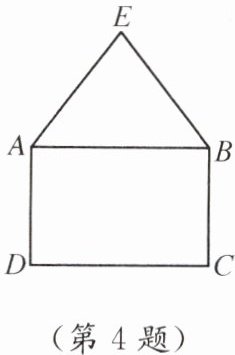
4. 如图,在长方形ABCD中,已知AB= 6,AD= 4,在长方形ABCD外画△ABE,使得AE= BE= 5,请建立适当的平面直角坐标系,并写出各顶点的坐标.

答案:解:以AB所在直线为x轴,AB的中点为原点建立平面直角坐标系。
∵AB=6,∴A(-3,0),B(3,0)。
∵AE=BE=5,设E(0,y),y>0,
由勾股定理得:3²+y²=5²,解得y=4,∴E(0,4)。
∵AD=4,∴D(-3,-4),C(3,-4)。
各顶点坐标为:A(-3,0),B(3,0),C(3,-4),D(-3,-4),E(0,4)。
∵AB=6,∴A(-3,0),B(3,0)。
∵AE=BE=5,设E(0,y),y>0,
由勾股定理得:3²+y²=5²,解得y=4,∴E(0,4)。
∵AD=4,∴D(-3,-4),C(3,-4)。
各顶点坐标为:A(-3,0),B(3,0),C(3,-4),D(-3,-4),E(0,4)。
5. 在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-4,5),B(-5,2),C(-1,3).
(1)①△A₀B₀C₀与△ABC关于y轴对称,在图①中画出△A₀B₀C₀,并写出△A₀B₀C₀三个顶点的坐标;$A_0(4,5)$,$B_0(5,2)$,$C_0(1,3)$
②观察图中对应点坐标之间的关系,写出平面直角坐标系中任意一点P(a,b)关于y轴的对称点的坐标:

(2)①直线$l_1$经过点(1,0),并且与y轴平行$,△A_1B_1C_1$与△ABC关于直线$l_1$对称,在图②中画出$△A_1B_1C_1,$并写出$△A_1B_1C_1$三个顶点的坐标.$A_1(6,5)$,$B_1(7,2)$,$C_1(3,3)$
②比较图②中$△A_1B_1C_1$与图①中△A₀B₀C₀的位置关系,你发现了什么?$△A_1B_1C_1$与$△A_0B_0C_0$关于x轴对称
③写出平面直角坐标系中任意一点P(a,b)关于直线$l_1$的对称点的坐标:
(3)如果要继续探究,你还能提出哪些问题?针对你提出的问题,请分别写出你的结论.问题:如果$\triangle ABC$关于直线$x = m$对称得到$\triangle A_2B_2C_2$,那么$\triangle A_2B_2C_2$三个顶点的坐标分别是多少?结论:$\triangle A_2B_2C_2$三个顶点坐标分别为$A_2(2m - x_A,y_A)$,$B_2(2m - x_B,y_B)$,$C_2(2m - x_C,y_C)$。
(1)①△A₀B₀C₀与△ABC关于y轴对称,在图①中画出△A₀B₀C₀,并写出△A₀B₀C₀三个顶点的坐标;$A_0(4,5)$,$B_0(5,2)$,$C_0(1,3)$
②观察图中对应点坐标之间的关系,写出平面直角坐标系中任意一点P(a,b)关于y轴的对称点的坐标:
$(-a,b)$
.
(2)①直线$l_1$经过点(1,0),并且与y轴平行$,△A_1B_1C_1$与△ABC关于直线$l_1$对称,在图②中画出$△A_1B_1C_1,$并写出$△A_1B_1C_1$三个顶点的坐标.$A_1(6,5)$,$B_1(7,2)$,$C_1(3,3)$
②比较图②中$△A_1B_1C_1$与图①中△A₀B₀C₀的位置关系,你发现了什么?$△A_1B_1C_1$与$△A_0B_0C_0$关于x轴对称
③写出平面直角坐标系中任意一点P(a,b)关于直线$l_1$的对称点的坐标:
$(2 - a,b)$
.(3)如果要继续探究,你还能提出哪些问题?针对你提出的问题,请分别写出你的结论.问题:如果$\triangle ABC$关于直线$x = m$对称得到$\triangle A_2B_2C_2$,那么$\triangle A_2B_2C_2$三个顶点的坐标分别是多少?结论:$\triangle A_2B_2C_2$三个顶点坐标分别为$A_2(2m - x_A,y_A)$,$B_2(2m - x_B,y_B)$,$C_2(2m - x_C,y_C)$。
答案:【解析】:本题主要考查了平面直角坐标系中图形的对称变换以及对称点坐标的求解。
(1)①关于$y$轴对称的点,纵坐标不变,横坐标互为相反数。
已知$A(-4,5)$,$B(-5,2)$,$C(-1,3)$,则$A_0(4,5)$,$B_0(5,2)$,$C_0(1,3)$。
在图①中,根据上述坐标描出$A_0$、$B_0$、$C_0$三点,然后顺次连接即可得到$\triangle A_0B_0C_0$。
②对于平面直角坐标系中任意一点$P(a,b)$,关于$y$轴的对称点,纵坐标不变,横坐标变为原来的相反数,所以对称点的坐标为$(-a,b)$。
(2)①关于直线$x = 1$对称的点,纵坐标不变,横坐标与$1$的距离相等且在直线$x = 1$的两侧。
点$A(-4,5)$到直线$x = 1$的距离为$\vert -4 - 1\vert = 5$,则其对称点$A_1$的横坐标为$1 + 5 = 6$,纵坐标不变,即$A_1(6,5)$。
点$B(-5,2)$到直线$x = 1$的距离为$\vert -5 - 1\vert = 6$,则其对称点$B_1$的横坐标为$1 + 6 = 7$,纵坐标不变,即$B_1(7,2)$。
点$C(-1,3)$到直线$x = 1$的距离为$\vert -1 - 1\vert = 2$,则其对称点$C_1$的横坐标为$1 + 2 = 3$,纵坐标不变,即$C_1(3,3)$。
在图②中,根据上述坐标描出$A_1$、$B_1$、$C_1$三点,然后顺次连接即可得到$\triangle A_1B_1C_1$。
②观察图②中$\triangle A_1B_1C_1$与图①中$\triangle A_0B_0C_0$的位置关系,发现它们关于$x$轴对称(通过对比对应点坐标可知)。
③对于平面直角坐标系中任意一点$P(a,b)$,设其关于直线$x = 1$的对称点为$P'(x,b)$。
根据对称性质,$\frac{a + x}{2} = 1$,解得$x = 2 - a$,所以对称点的坐标为$(2 - a,b)$。
(3)提出的问题及结论如下:
问题:如果$\triangle ABC$关于直线$x = m$对称得到$\triangle A_2B_2C_2$,那么$\triangle A_2B_2C_2$三个顶点的坐标分别是多少?
结论:设$\triangle ABC$三个顶点坐标分别为$A(x_A,y_A)$,$B(x_B,y_B)$,$C(x_C,y_C)$,则$\triangle A_2B_2C_2$三个顶点坐标分别为$A_2(2m - x_A,y_A)$,$B_2(2m - x_B,y_B)$,$C_2(2m - x_C,y_C)$。
【答案】:
(1)①图略;$A_0(4,5)$,$B_0(5,2)$,$C_0(1,3)$;②$(-a,b)$;
(2)①图略;$A_1(6,5)$,$B_1(7,2)$,$C_1(3,3)$;②$\triangle A_1B_1C_1$与$\triangle A_0B_0C_0$关于$x$轴对称;③$(2 - a,b)$;
(3)问题:如果$\triangle ABC$关于直线$x = m$对称得到$\triangle A_2B_2C_2$,那么$\triangle A_2B_2C_2$三个顶点的坐标分别是多少?
结论:$\triangle A_2B_2C_2$三个顶点坐标分别为$A_2(2m - x_A,y_A)$,$B_2(2m - x_B,y_B)$,$C_2(2m - x_C,y_C)$。
(1)①关于$y$轴对称的点,纵坐标不变,横坐标互为相反数。
已知$A(-4,5)$,$B(-5,2)$,$C(-1,3)$,则$A_0(4,5)$,$B_0(5,2)$,$C_0(1,3)$。
在图①中,根据上述坐标描出$A_0$、$B_0$、$C_0$三点,然后顺次连接即可得到$\triangle A_0B_0C_0$。
②对于平面直角坐标系中任意一点$P(a,b)$,关于$y$轴的对称点,纵坐标不变,横坐标变为原来的相反数,所以对称点的坐标为$(-a,b)$。
(2)①关于直线$x = 1$对称的点,纵坐标不变,横坐标与$1$的距离相等且在直线$x = 1$的两侧。
点$A(-4,5)$到直线$x = 1$的距离为$\vert -4 - 1\vert = 5$,则其对称点$A_1$的横坐标为$1 + 5 = 6$,纵坐标不变,即$A_1(6,5)$。
点$B(-5,2)$到直线$x = 1$的距离为$\vert -5 - 1\vert = 6$,则其对称点$B_1$的横坐标为$1 + 6 = 7$,纵坐标不变,即$B_1(7,2)$。
点$C(-1,3)$到直线$x = 1$的距离为$\vert -1 - 1\vert = 2$,则其对称点$C_1$的横坐标为$1 + 2 = 3$,纵坐标不变,即$C_1(3,3)$。
在图②中,根据上述坐标描出$A_1$、$B_1$、$C_1$三点,然后顺次连接即可得到$\triangle A_1B_1C_1$。
②观察图②中$\triangle A_1B_1C_1$与图①中$\triangle A_0B_0C_0$的位置关系,发现它们关于$x$轴对称(通过对比对应点坐标可知)。
③对于平面直角坐标系中任意一点$P(a,b)$,设其关于直线$x = 1$的对称点为$P'(x,b)$。
根据对称性质,$\frac{a + x}{2} = 1$,解得$x = 2 - a$,所以对称点的坐标为$(2 - a,b)$。
(3)提出的问题及结论如下:
问题:如果$\triangle ABC$关于直线$x = m$对称得到$\triangle A_2B_2C_2$,那么$\triangle A_2B_2C_2$三个顶点的坐标分别是多少?
结论:设$\triangle ABC$三个顶点坐标分别为$A(x_A,y_A)$,$B(x_B,y_B)$,$C(x_C,y_C)$,则$\triangle A_2B_2C_2$三个顶点坐标分别为$A_2(2m - x_A,y_A)$,$B_2(2m - x_B,y_B)$,$C_2(2m - x_C,y_C)$。
【答案】:
(1)①图略;$A_0(4,5)$,$B_0(5,2)$,$C_0(1,3)$;②$(-a,b)$;
(2)①图略;$A_1(6,5)$,$B_1(7,2)$,$C_1(3,3)$;②$\triangle A_1B_1C_1$与$\triangle A_0B_0C_0$关于$x$轴对称;③$(2 - a,b)$;
(3)问题:如果$\triangle ABC$关于直线$x = m$对称得到$\triangle A_2B_2C_2$,那么$\triangle A_2B_2C_2$三个顶点的坐标分别是多少?
结论:$\triangle A_2B_2C_2$三个顶点坐标分别为$A_2(2m - x_A,y_A)$,$B_2(2m - x_B,y_B)$,$C_2(2m - x_C,y_C)$。