3. 求下列函数中自变量x的取值范围:
(1) $ y= 2x+1 $;
(2) $ y= \frac{1}{x} $;
(3) $ y= \sqrt{x-1} $.
(1) $ y= 2x+1 $;
(2) $ y= \frac{1}{x} $;
(3) $ y= \sqrt{x-1} $.
答案:【解析】:
本题主要考察函数自变量取值范围的求解。对于不同类型的函数,其自变量的取值范围会有所不同。
(1) 对于一次函数 $y = 2x + 1$,其自变量 $x$ 可以取全体实数,因为一次函数的定义域是全体实数。
(2) 对于反比例函数 $y = \frac{1}{x}$,其自变量 $x$ 不能为0,因为0不能作为分母。
(3) 对于根式函数 $y = \sqrt{x - 1}$,其自变量 $x$ 必须满足 $x - 1 \geq 0$,以保证根式内部非负。
【答案】:
(1) $x$ 取全体实数;
(2) $x \neq 0$;
(3) $x \geq 1$。
本题主要考察函数自变量取值范围的求解。对于不同类型的函数,其自变量的取值范围会有所不同。
(1) 对于一次函数 $y = 2x + 1$,其自变量 $x$ 可以取全体实数,因为一次函数的定义域是全体实数。
(2) 对于反比例函数 $y = \frac{1}{x}$,其自变量 $x$ 不能为0,因为0不能作为分母。
(3) 对于根式函数 $y = \sqrt{x - 1}$,其自变量 $x$ 必须满足 $x - 1 \geq 0$,以保证根式内部非负。
【答案】:
(1) $x$ 取全体实数;
(2) $x \neq 0$;
(3) $x \geq 1$。
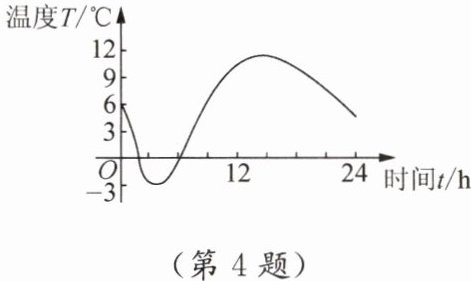
4. 如图,对于某一天每一个确定的时刻,是否都相应地确定一个温度?哪个变量是另一个变量的函数?

答案:【解析】:
本题考查函数的概念。
根据函数的定义,对于自变量的每一个确定的值,因变量都有唯一确定的值与其对应。
在本题中,时刻是自变量,温度是因变量。
对于某一天每一个确定的时刻,气温是确定的,因此每一个时刻都相应地确定一个温度。
所以,温度是时间的函数。
【答案】:
对于某一天每一个确定的时刻,都相应地确定一个温度;
变量$T$是变量$t$的函数。
本题考查函数的概念。
根据函数的定义,对于自变量的每一个确定的值,因变量都有唯一确定的值与其对应。
在本题中,时刻是自变量,温度是因变量。
对于某一天每一个确定的时刻,气温是确定的,因此每一个时刻都相应地确定一个温度。
所以,温度是时间的函数。
【答案】:
对于某一天每一个确定的时刻,都相应地确定一个温度;
变量$T$是变量$t$的函数。
5. 在国内投寄平信应付邮资如下表.

(1) y是关于x的函数吗?为什么?
(2) 当x= 5,10,30,50时,分别求函数值,并说明它们的实际意义.

(1) y是关于x的函数吗?为什么?
(2) 当x= 5,10,30,50时,分别求函数值,并说明它们的实际意义.
答案:
(1)解:y是关于x的函数。因为对于x在给定范围内的每一个值,y都有唯一确定的值与之对应。
(2)解:当x=5时,0<5≤20,y=1.20,实际意义为质量为5g的平信应付邮资1.20元;
当x=10时,0<10≤20,y=1.20,实际意义为质量为10g的平信应付邮资1.20元;
当x=30时,20<30≤40,y=2.40,实际意义为质量为30g的平信应付邮资2.40元;
当x=50时,40<50≤60,y=3.60,实际意义为质量为50g的平信应付邮资3.60元。
(1)解:y是关于x的函数。因为对于x在给定范围内的每一个值,y都有唯一确定的值与之对应。
(2)解:当x=5时,0<5≤20,y=1.20,实际意义为质量为5g的平信应付邮资1.20元;
当x=10时,0<10≤20,y=1.20,实际意义为质量为10g的平信应付邮资1.20元;
当x=30时,20<30≤40,y=2.40,实际意义为质量为30g的平信应付邮资2.40元;
当x=50时,40<50≤60,y=3.60,实际意义为质量为50g的平信应付邮资3.60元。
6. 如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10 cm,边CA和边MN在一条直线上,点A与点M重合.△ABC沿MN方向运动,当点A与点N重合时停止运动.运动中两个图形重叠部分的面积为$y cm^2,MA$的长度为x cm,用含x的式子表示y,并写出x的取值范围.


答案:【解析】:本题考查根据实际问题列二次函数关系式,关键是得到重叠部分三角形的底与高与$MA$的长度的关系。
当$\bigtriangleup ABC$向右移动时,重叠部分的底为$x$,高随着底的变化而变化,根据三角形的面积公式就可以求出$y$与$x$的关系式,根据$MA$的长度就可以求出$x$的取值范围。
【答案】:解:由题意得
重叠部分三角形的底为$x$,高为$x$,
所以重叠部分三角形的面积为:
$y=\frac{1}{2}x^2$,
因为$AM$由$0$到$10cm$,
所以$x$的取值范围为$0\leq x\leq10$。
当$\bigtriangleup ABC$向右移动时,重叠部分的底为$x$,高随着底的变化而变化,根据三角形的面积公式就可以求出$y$与$x$的关系式,根据$MA$的长度就可以求出$x$的取值范围。
【答案】:解:由题意得
重叠部分三角形的底为$x$,高为$x$,
所以重叠部分三角形的面积为:
$y=\frac{1}{2}x^2$,
因为$AM$由$0$到$10cm$,
所以$x$的取值范围为$0\leq x\leq10$。