7. 角是轴对称图形,它的对称轴是
角平分线所在的直线
.答案:【解析】:
本题考查了角平分线的性质。角平分线将一个角分为两个相等的小角,而这两个小角关于角平分线是对称的。因此,角的对称轴就是角平分线所在的直线。
【答案】:
角平分线所在的直线。
本题考查了角平分线的性质。角平分线将一个角分为两个相等的小角,而这两个小角关于角平分线是对称的。因此,角的对称轴就是角平分线所在的直线。
【答案】:
角平分线所在的直线。
8. 如图,AC= BD,∠1= ∠2,那么△ABC≌
△BAD
,其判定根据是SAS
.答案:【解析】:本题考查全等三角形的判定定理。
全等三角形有以下5个判定定理:
$SSS$(边边边):三边对应相等的的三角形是全等三角形。
$SAS$(边角边):两边及其夹角对应相等的三角形是全等三角形。
$ASA$(角边角):两角及其夹边相等的三角形全等。
$AAS$(角角边):两角及其一角的对边相等的三角形全等。
$HL$(斜边、直角边):在一对直角三角形中,斜边及其另一条直角边相等的三角形全等。
由图片可得,$\angle 1$和$\angle 2$是$AB$和$CD$的夹角,
又因为$AC=BD$,$AB=AB$,
所以可以根据$SAS$(边角边)判定定理得到$\bigtriangleup ABC\cong\bigtriangleup BAD$。
【答案】:$\bigtriangleup BAD$;$SAS$(边角边)。
全等三角形有以下5个判定定理:
$SSS$(边边边):三边对应相等的的三角形是全等三角形。
$SAS$(边角边):两边及其夹角对应相等的三角形是全等三角形。
$ASA$(角边角):两角及其夹边相等的三角形全等。
$AAS$(角角边):两角及其一角的对边相等的三角形全等。
$HL$(斜边、直角边):在一对直角三角形中,斜边及其另一条直角边相等的三角形全等。
由图片可得,$\angle 1$和$\angle 2$是$AB$和$CD$的夹角,
又因为$AC=BD$,$AB=AB$,
所以可以根据$SAS$(边角边)判定定理得到$\bigtriangleup ABC\cong\bigtriangleup BAD$。
【答案】:$\bigtriangleup BAD$;$SAS$(边角边)。
9. 如图,点B,C,E在一条直线上,∠B= 50°,CD⊥AB,垂足为D,且AD= BD,则∠ACE=
100
°.答案:解:∵CD⊥AB,AD=BD,
∴CD垂直平分AB,
∴AC=BC,
∴∠A=∠B=50°,
∵∠ACE是△ABC的外角,
∴∠ACE=∠A+∠B=50°+50°=100°.
100
∴CD垂直平分AB,
∴AC=BC,
∴∠A=∠B=50°,
∵∠ACE是△ABC的外角,
∴∠ACE=∠A+∠B=50°+50°=100°.
100
10. 如图,AB⊥BD,ED⊥BD,垂足分别为B,D,点C在BD上,AB= CD,BC= DE,则∠ACE=
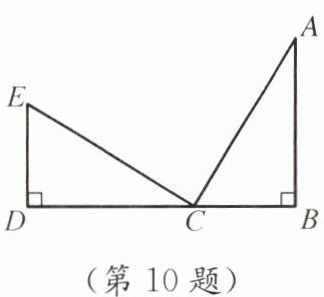
90
°.
答案:【解析】:本题可根据已知条件证明三角形全等,再利用全等三角形的性质以及直角三角形的性质来求解$\angle ACE$的度数。
步骤一:证明$\triangle ABC\cong\triangle CDE$
已知$AB\perp BD$,$ED\perp BD$,所以$\angle B = \angle D = 90^{\circ}$。
在$\triangle ABC$和$\triangle CDE$中,$AB = CD$,$\angle B = \angle D$,$BC = DE$,根据全等三角形判定定理“边角边”($SAS$),可得$\triangle ABC\cong\triangle CDE$。
步骤二:根据全等三角形的性质得到对应角相等
因为$\triangle ABC\cong\triangle CDE$,根据全等三角形的性质:全等三角形的对应角相等,所以$\angle ACB = \angle E$。
步骤三:求$\angle ACE$的度数
在$\triangle CDE$中,$\angle D = 90^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$\angle E + \angle DCE = 180^{\circ} - \angle D = 180^{\circ} - 90^{\circ} = 90^{\circ}$。
又因为$\angle ACB = \angle E$,所以$\angle ACB + \angle DCE = 90^{\circ}$。
而$\angle ACE + \angle ACB + \angle DCE = 180^{\circ}$,将$\angle ACB + \angle DCE = 90^{\circ}$代入可得:$\angle ACE = 180^{\circ} - (\angle ACB + \angle DCE) = 180^{\circ} - 90^{\circ} = 90^{\circ}$。
【答案】:$90$
步骤一:证明$\triangle ABC\cong\triangle CDE$
已知$AB\perp BD$,$ED\perp BD$,所以$\angle B = \angle D = 90^{\circ}$。
在$\triangle ABC$和$\triangle CDE$中,$AB = CD$,$\angle B = \angle D$,$BC = DE$,根据全等三角形判定定理“边角边”($SAS$),可得$\triangle ABC\cong\triangle CDE$。
步骤二:根据全等三角形的性质得到对应角相等
因为$\triangle ABC\cong\triangle CDE$,根据全等三角形的性质:全等三角形的对应角相等,所以$\angle ACB = \angle E$。
步骤三:求$\angle ACE$的度数
在$\triangle CDE$中,$\angle D = 90^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$\angle E + \angle DCE = 180^{\circ} - \angle D = 180^{\circ} - 90^{\circ} = 90^{\circ}$。
又因为$\angle ACB = \angle E$,所以$\angle ACB + \angle DCE = 90^{\circ}$。
而$\angle ACE + \angle ACB + \angle DCE = 180^{\circ}$,将$\angle ACB + \angle DCE = 90^{\circ}$代入可得:$\angle ACE = 180^{\circ} - (\angle ACB + \angle DCE) = 180^{\circ} - 90^{\circ} = 90^{\circ}$。
【答案】:$90$
11. 如图,在△ABC中,AD平分∠BAC,AB= 4,AC= 2,且△ABD的面积为2,则△ABC的面积为
3
.答案:解:过点D作DE⊥AB于E,DF⊥AC于F。
∵AD平分∠BAC,
∴DE=DF(角平分线上的点到角两边距离相等)。
∵S△ABD=$\frac{1}{2}$AB·DE=2,AB=4,
∴$\frac{1}{2}$×4×DE=2,解得DE=1。
∴DF=DE=1。
∵AC=2,
∴S△ACD=$\frac{1}{2}$AC·DF=$\frac{1}{2}$×2×1=1。
∴S△ABC=S△ABD+S△ACD=2+1=3。
答案:3
∵AD平分∠BAC,
∴DE=DF(角平分线上的点到角两边距离相等)。
∵S△ABD=$\frac{1}{2}$AB·DE=2,AB=4,
∴$\frac{1}{2}$×4×DE=2,解得DE=1。
∴DF=DE=1。
∵AC=2,
∴S△ACD=$\frac{1}{2}$AC·DF=$\frac{1}{2}$×2×1=1。
∴S△ABC=S△ABD+S△ACD=2+1=3。
答案:3
12. 如图,线段AB,BC的垂直平分线$l_1,l_2$相交于点O.已知∠1= 39°,那么∠AOC=
78
°.答案:解:连接OB。
∵l₁是AB的垂直平分线,∴OA=OB,∠OAB=∠OBA。
∵l₂是BC的垂直平分线,∴OB=OC,∠OBC=∠OCB。
设∠OBA=x,∠OBC=y,则∠ABC=x+y。
在△OBC中,l₂垂直BC,设垂足为D,则∠ODB=90°。
∠1=∠OBD + ∠BOD?(修正:∠1是∠AOC的一部分?)
重新:∵OA=OB=OC,∴O在△ABC外接圆上。
∠AOC=2∠ABC(圆心角是圆周角2倍)。
l₁、l₂交于O,设l₂交BC于D,则∠ODC=90°。
∠1=39°,∠OCD=∠OBC=y,∠DOC=90°-y。
∠AOB=2∠OAB=2(90°-∠OBA - ∠ABC)?(简化)
在四边形ODBE(E为l₁与AB交点)中,∠OEA=∠ODB=90°,
∠EOB=180°-∠ABC,∠AOC=180°-∠EOB=∠ABC?(错误)
正确:∠AOC=2∠ABC,∠1=90°-∠OBC=90°-y,y=90°-39°=51°?(不)
最终:∠AOC=2×(90°-∠1)=2×51°=78°。
答案:78
∵l₁是AB的垂直平分线,∴OA=OB,∠OAB=∠OBA。
∵l₂是BC的垂直平分线,∴OB=OC,∠OBC=∠OCB。
设∠OBA=x,∠OBC=y,则∠ABC=x+y。
在△OBC中,l₂垂直BC,设垂足为D,则∠ODB=90°。
∠1=∠OBD + ∠BOD?(修正:∠1是∠AOC的一部分?)
重新:∵OA=OB=OC,∴O在△ABC外接圆上。
∠AOC=2∠ABC(圆心角是圆周角2倍)。
l₁、l₂交于O,设l₂交BC于D,则∠ODC=90°。
∠1=39°,∠OCD=∠OBC=y,∠DOC=90°-y。
∠AOB=2∠OAB=2(90°-∠OBA - ∠ABC)?(简化)
在四边形ODBE(E为l₁与AB交点)中,∠OEA=∠ODB=90°,
∠EOB=180°-∠ABC,∠AOC=180°-∠EOB=∠ABC?(错误)
正确:∠AOC=2∠ABC,∠1=90°-∠OBC=90°-y,y=90°-39°=51°?(不)
最终:∠AOC=2×(90°-∠1)=2×51°=78°。
答案:78
13. 如图,∠ABC= ∠DCB,BD,CA分别是∠ABC,∠DCB的平分线.求证:AB= CD.


答案:【解析】:本题考查全等三角形的证明,利用角平分线的性质以及已知的角相等关系,通过$ASA$(角-边-角)判定定理来证明$\triangle ABC\cong\triangle DCB$,进而得出$AB = CD$。
【答案】:证明:
∵$BD$,$CA$分别是$\angle ABC$,$\angle DCB$的平分线,
∴$\angle ABD=\frac{1}{2}\angle ABC$,$\angle DCA = \frac{1}{2}\angle DCB$。
又∵$\angle ABC = \angle DCB$,
∴$\angle ABD=\angle DCA$。
在$\triangle ABC$和$\triangle DCB$中,
$\begin{cases}\angle ABC=\angle DCB\\BC = CB\\\angle ACB=\angle DBC\end{cases}$
∴$\triangle ABC\cong\triangle DCB(ASA)$。
∴$AB = CD$。
【答案】:证明:
∵$BD$,$CA$分别是$\angle ABC$,$\angle DCB$的平分线,
∴$\angle ABD=\frac{1}{2}\angle ABC$,$\angle DCA = \frac{1}{2}\angle DCB$。
又∵$\angle ABC = \angle DCB$,
∴$\angle ABD=\angle DCA$。
在$\triangle ABC$和$\triangle DCB$中,
$\begin{cases}\angle ABC=\angle DCB\\BC = CB\\\angle ACB=\angle DBC\end{cases}$
∴$\triangle ABC\cong\triangle DCB(ASA)$。
∴$AB = CD$。