17. 请利用直尺和圆规用两种不同的方法作∠O的平分线OC(不写作法,保留作图痕迹).
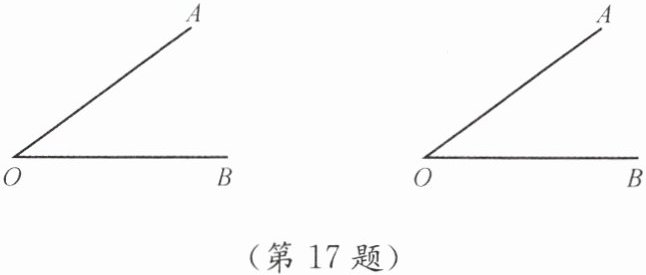

答案:【解析】:
本题考查了角平分线的作法,有两种常见的方法:
方法一:利用三边对应相等的三角形全等来作角平分线。
以$O$为圆心,任意长为半径画弧,分别交$OA$、$OB$于两点;
再分别以这两个交点为圆心,大于两交点距离一半的长度为半径画弧,两弧相交于一点;
连接$O$与该交点,这条线就是$\angle AOB$的平分线。
方法二:利用等腰三角形三线合一的性质来作角平分线。
在$OA$、$OB$上分别截取相等的两段$OD$、$OE$;
连接$DE$,作$DE$的垂直平分线交$\angle AOB$于点$C$;
连接$OC$,$OC$就是$\angle AOB$的平分线。
【答案】:
图略(按照上述两种方法的描述,使用直尺和圆规作出$\angle AOB$的平分线$OC$,保留作图痕迹即可)。
本题考查了角平分线的作法,有两种常见的方法:
方法一:利用三边对应相等的三角形全等来作角平分线。
以$O$为圆心,任意长为半径画弧,分别交$OA$、$OB$于两点;
再分别以这两个交点为圆心,大于两交点距离一半的长度为半径画弧,两弧相交于一点;
连接$O$与该交点,这条线就是$\angle AOB$的平分线。
方法二:利用等腰三角形三线合一的性质来作角平分线。
在$OA$、$OB$上分别截取相等的两段$OD$、$OE$;
连接$DE$,作$DE$的垂直平分线交$\angle AOB$于点$C$;
连接$OC$,$OC$就是$\angle AOB$的平分线。
【答案】:
图略(按照上述两种方法的描述,使用直尺和圆规作出$\angle AOB$的平分线$OC$,保留作图痕迹即可)。
18. 如图,在△ABC中,CD⊥BD,垂足为D,且CD= BD.BE平分∠ABC,且BE⊥AC,垂足为E,交CD于点F.
(1) 求证:AE= CE;
(2) 求证:BF= 2CE.

(1) 求证:AE= CE;
(2) 求证:BF= 2CE.

答案:【解析】:
(1) 证明:
∵$BE⊥AC$,
∴$\angle BEA = \angle BEC = 90^\circ$,
在$\triangle BAE$和$\triangle BCE$中,
$\angle ABE = \angle CBE$($BE$平分$\angle ABC$),
$BE = BE$(公共边),
$\angle BEA = \angle BEC$,
∴$\triangle BAE \cong \triangle BCE$($ASA$),
∴$AE = CE$。
(2) 证明:
∵$CD \perp AB$,$BE \perp AC$,
∴$\angle CDA = \angle BDA = \angle BEA = 90^\circ$,
∴$\angle ACD + \angle CAD = 90^\circ$,$\angle ABE + \angle CAD = 90^\circ$,
∴$\angle ACD = \angle ABE$,
在$\triangle BDF$和$\triangle CDA$中,
$\angle BDF = \angle CDA$,
$BD = CD$,
$\angle ACD = \angle ABE$,
∴$\triangle BDF \cong \triangle CDA$($ASA$),
∴$BF = AC$,
∵$AE = CE$,
∴$AC = 2CE$,
∴$BF = 2CE$。
【答案】:
(1) 证明见解析;
(2) 证明见解析。
(1) 证明:
∵$BE⊥AC$,
∴$\angle BEA = \angle BEC = 90^\circ$,
在$\triangle BAE$和$\triangle BCE$中,
$\angle ABE = \angle CBE$($BE$平分$\angle ABC$),
$BE = BE$(公共边),
$\angle BEA = \angle BEC$,
∴$\triangle BAE \cong \triangle BCE$($ASA$),
∴$AE = CE$。
(2) 证明:
∵$CD \perp AB$,$BE \perp AC$,
∴$\angle CDA = \angle BDA = \angle BEA = 90^\circ$,
∴$\angle ACD + \angle CAD = 90^\circ$,$\angle ABE + \angle CAD = 90^\circ$,
∴$\angle ACD = \angle ABE$,
在$\triangle BDF$和$\triangle CDA$中,
$\angle BDF = \angle CDA$,
$BD = CD$,
$\angle ACD = \angle ABE$,
∴$\triangle BDF \cong \triangle CDA$($ASA$),
∴$BF = AC$,
∵$AE = CE$,
∴$AC = 2CE$,
∴$BF = 2CE$。
【答案】:
(1) 证明见解析;
(2) 证明见解析。
19. 如图,在△ABC中,AD为中线.求证:AB+AC>2AD.


答案:【解析】:
本题可根据三角形三边关系,通过延长$AD$构造全等三角形,将$AB$、$AC$、$AD$转化到同一个三角形中,进而证明$AB + AC\gt 2AD$。
步骤一:延长$AD$至点$E$,使$DE = AD$,连接$BE$。
因为$AD$是$\triangle ABC$的中线,所以$BD = CD$。
在$\triangle BDE$和$\triangle CDA$中:
$\begin{cases}BD = CD\\\angle BDE = \angle CDA\\DE = DA\end{cases}$
根据“边角边”($SAS$)判定定理,可得$\triangle BDE\cong\triangle CDA$。
步骤二:根据全等三角形的性质得到$BE$与$AC$的关系。
由$\triangle BDE\cong\triangle CDA$,根据全等三角形的对应边相等,可得$BE = AC$。
步骤三:在$\triangle ABE$中利用三角形三边关系得到$AB + BE\gt AE$。
因为$AE = AD + DE$,且$DE = AD$,所以$AE = 2AD$。
又因为$BE = AC$,所以$AB + AC = AB + BE$。
根据三角形三边关系“两边之和大于第三边”,在$\triangle ABE$中,$AB + BE\gt AE$,即$AB + AC\gt 2AD$。
【答案】:
证明:延长$AD$至点$E$,使$DE = AD$,连接$BE$。
$\because AD$是$\triangle ABC$的中线,
$\therefore BD = CD$。
在$\triangle BDE$和$\triangle CDA$中,
$\begin{cases}BD = CD\\\angle BDE = \angle CDA\\DE = DA\end{cases}$
$\therefore \triangle BDE\cong\triangle CDA(SAS)$。
$\therefore BE = AC$。
在$\triangle ABE$中,$AB + BE\gt AE$。
$\because AE = AD + DE = 2AD$,$BE = AC$,
$\therefore AB + AC\gt 2AD$。
本题可根据三角形三边关系,通过延长$AD$构造全等三角形,将$AB$、$AC$、$AD$转化到同一个三角形中,进而证明$AB + AC\gt 2AD$。
步骤一:延长$AD$至点$E$,使$DE = AD$,连接$BE$。
因为$AD$是$\triangle ABC$的中线,所以$BD = CD$。
在$\triangle BDE$和$\triangle CDA$中:
$\begin{cases}BD = CD\\\angle BDE = \angle CDA\\DE = DA\end{cases}$
根据“边角边”($SAS$)判定定理,可得$\triangle BDE\cong\triangle CDA$。
步骤二:根据全等三角形的性质得到$BE$与$AC$的关系。
由$\triangle BDE\cong\triangle CDA$,根据全等三角形的对应边相等,可得$BE = AC$。
步骤三:在$\triangle ABE$中利用三角形三边关系得到$AB + BE\gt AE$。
因为$AE = AD + DE$,且$DE = AD$,所以$AE = 2AD$。
又因为$BE = AC$,所以$AB + AC = AB + BE$。
根据三角形三边关系“两边之和大于第三边”,在$\triangle ABE$中,$AB + BE\gt AE$,即$AB + AC\gt 2AD$。
【答案】:
证明:延长$AD$至点$E$,使$DE = AD$,连接$BE$。
$\because AD$是$\triangle ABC$的中线,
$\therefore BD = CD$。
在$\triangle BDE$和$\triangle CDA$中,
$\begin{cases}BD = CD\\\angle BDE = \angle CDA\\DE = DA\end{cases}$
$\therefore \triangle BDE\cong\triangle CDA(SAS)$。
$\therefore BE = AC$。
在$\triangle ABE$中,$AB + BE\gt AE$。
$\because AE = AD + DE = 2AD$,$BE = AC$,
$\therefore AB + AC\gt 2AD$。
如图,在△ABC中,AD⊥BC,垂足为D.小莉说:当AB+BD= AC+CD时,△ABC是等腰三角形.她的说法正确吗?如正确,请证明;如不正确,请举反例说明.


答案:【解析】:
本题考查了等腰三角形的性质及勾股定理的应用,通过给定的条件$AB+BD=AC+CD$,结合垂直关系,利用勾股定理将$AB$,$AC$用$BD$,$CD$及$AD$表示出来,然后通过等式变形和化简,推导出$BD=CD$,进而证明$\bigtriangleup ABC$是等腰三角形。
【答案】:
解:小莉的说法正确,
证明:
∵$AD\bot BC$,
∴$\angle ADB=\angle ADC=90^{\circ}$,
在$Rt\bigtriangleup ABD$和$Rt\bigtriangleup ACD$中,
根据勾股定理可得$AB^{2}-BD^{2}=AD^{2}$,$AC^{2}-CD^{2}=AD^{2}$,
∴$AB^{2}-BD^{2}=AC^{2}-CD^{2}$,即$AB^{2}-AC^{2}=BD^{2}-CD^{2}$,
∵$AB+BD=AC+CD$,
∴$AB-AC=BD-CD$,
∵$AB^{2}-AC^{2}=(AB+AC)(AB-AC)$,$BD^{2}-CD^{2}=(BD+CD)(BD-CD)$,
∴$(AB+AC)(AB-AC)=(BD+CD)(BD-CD)$,
∴$\frac{AB-AC}{AB+AC}=\frac{BD-CD}{BD+CD}$,
又∵$AB-AC=BD-CD$,
∴$AB+AC=BD+CD$,
联立$\begin{cases}AB+BD=AC+CD,\\AB+AC=BD+CD.\end{cases}$
两式相减得:$BD-AC=AC-BD$,
移项可得$2BD=2AC$,即$BD=CD$,
∵$AD\bot BC$,$BD=CD$,
∴$AD$是$BC$的垂直平分线,
根据等腰三角形三线合一的性质可知$\bigtriangleup ABC$是等腰三角形。
本题考查了等腰三角形的性质及勾股定理的应用,通过给定的条件$AB+BD=AC+CD$,结合垂直关系,利用勾股定理将$AB$,$AC$用$BD$,$CD$及$AD$表示出来,然后通过等式变形和化简,推导出$BD=CD$,进而证明$\bigtriangleup ABC$是等腰三角形。
【答案】:
解:小莉的说法正确,
证明:
∵$AD\bot BC$,
∴$\angle ADB=\angle ADC=90^{\circ}$,
在$Rt\bigtriangleup ABD$和$Rt\bigtriangleup ACD$中,
根据勾股定理可得$AB^{2}-BD^{2}=AD^{2}$,$AC^{2}-CD^{2}=AD^{2}$,
∴$AB^{2}-BD^{2}=AC^{2}-CD^{2}$,即$AB^{2}-AC^{2}=BD^{2}-CD^{2}$,
∵$AB+BD=AC+CD$,
∴$AB-AC=BD-CD$,
∵$AB^{2}-AC^{2}=(AB+AC)(AB-AC)$,$BD^{2}-CD^{2}=(BD+CD)(BD-CD)$,
∴$(AB+AC)(AB-AC)=(BD+CD)(BD-CD)$,
∴$\frac{AB-AC}{AB+AC}=\frac{BD-CD}{BD+CD}$,
又∵$AB-AC=BD-CD$,
∴$AB+AC=BD+CD$,
联立$\begin{cases}AB+BD=AC+CD,\\AB+AC=BD+CD.\end{cases}$
两式相减得:$BD-AC=AC-BD$,
移项可得$2BD=2AC$,即$BD=CD$,
∵$AD\bot BC$,$BD=CD$,
∴$AD$是$BC$的垂直平分线,
根据等腰三角形三线合一的性质可知$\bigtriangleup ABC$是等腰三角形。