答案：【解析】：
本题主要考查平方根和立方根的应用。
(1) 对于方程 $4x^2 = 81$，可以先将方程两边同时除以4，得到 $x^2 = \frac{81}{4}$。然后对方程两边同时开平方，即可求出x的值。
(2) 对于方程 $(x+1)^3 - 27 = 0$，可以先将方程移项，得到 $(x+1)^3 = 27$。然后对方程两边同时开立方，即可求出x的值。
【答案】：
(1) 解：
$4x^2 = 81$
$x^2 = \frac{81}{4}$
$x = \pm \sqrt{\frac{81}{4}}$
$x = \pm \frac{9}{2}$
(2) 解：
$(x+1)^3 - 27 = 0$
$(x+1)^3 = 27$
$x+1 = \sqrt[3]{27}$
$x+1 = 3$
$x = 2$

答案：【解析】：
本题主要考查了实数的大小比较，对于这类题目，我们可以采用以下方法：
(1) 对于 $\sqrt{5}$ 与 2.5 的比较，我们可以先计算它们的平方，然后比较平方的大小，因为平方函数在实数范围内是单调增函数，所以原数的大小关系与其平方的大小关系一致。
(2) 对于 $\sqrt[3]{-25}$ 与 -3 的比较，我们可以先计算它们的立方，然后比较立方的大小。同样地，因为立方函数在实数范围内也是单调增函数，在比较负数时，绝对值大的数实际上更小，所以原数的大小关系与其立方的大小关系一致。
(3) 对于 $\frac{\sqrt{5}-1}{2}$ 与 $\frac{1}{2}$ 的比较，我们可以先计算它们的差，然后判断差的符号。如果差大于0，则第一个数大于第二个数；如果差小于0，则第一个数小于第二个数；如果差等于0，则两个数相等。
【答案】：
(1) 解：
$(\sqrt{5})^2 = 5$，
$2.5^2 = 6.25$，
因为 $5 ＜ 6.25$，
所以 $\sqrt{5} ＜ 2.5$。
(2) 解：
$(\sqrt[3]{-25})^3 = -25$，
$(-3)^3 = -27$，
因为 $-25 ＞ -27$（注意这里是负数，绝对值大的数实际上更小），
所以 $\sqrt[3]{-25} ＞ -3$。
(3) 解：
$\frac{\sqrt{5}-1}{2} - \frac{1}{2} = \frac{\sqrt{5} - 1 - 1}{2} = \frac{\sqrt{5} - 2}{2}$，
因为 $\sqrt{5} ＞ 2$（$\sqrt{4} = 2$，而5大于4），
所以 $\frac{\sqrt{5} - 2}{2} ＞ 0$，
因此 $\frac{\sqrt{5}-1}{2} ＞ \frac{1}{2}$。

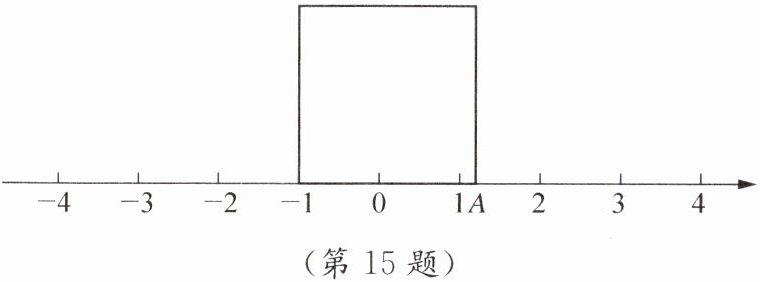
答案：解：∵正方形面积为x，
∴正方形边长为√x。
∵正方形一个顶点与数轴上表示-1的点重合，一条边落在数轴上，另一个顶点与点A重合，且点A在数轴正半轴，
∴点A表示的数为-1 + √x。
答：点A表示的数为√x - 1。

答案：【解析】：本题主要考查了实数与数轴以及勾股定理的应用。
（1）根据勾股定理，若直角三角形的两直角边分别为$a$和$b$，斜边为$c$，则有$a^2 + b^2 = c^2$。
在正方形$ABCD$中，$AB$作为半径，其长度可以通过勾股定理求得。
观察正方形$ABCD$，可知$A$点坐标为$(0,0)$，$B$点坐标为$(2,1)$。
因此，$AB$的长度为$\sqrt{(2-0)^2 + (1-0)^2} = \sqrt{4+1} = \sqrt{5}$。
所以，以原点为圆心，$AB$为半径画弧，与数轴正半轴的交点$E$表示的数就是$\sqrt{5}$。
（2）要找到数轴上表示$\sqrt{10}$的点，需要构造一个直角三角形，使得其斜边长度为$\sqrt{10}$。
观察网格，可以发现直角三角形的两直角边分别为$1$和$3$时，斜边长度为$\sqrt{1^2 + 3^2} = \sqrt{10}$。
因此，以正方形$ABCD$的顶点$D$为起点，向右水平移动$1$个单位，再向上垂直移动$3$个单位，到达点$F$。
连接$DF$，则$DF$的长度为$\sqrt{10}$。
以原点为圆心，$DF$为半径画弧，与数轴正半轴的交点即为表示$\sqrt{10}$的点。
（3）要画出表示$\sqrt{8}$的点，同样需要构造一个直角三角形，使得其斜边长度为$\sqrt{8}$。
观察网格，可以发现直角三角形的两直角边分别为$2$和$2$时，斜边长度为$\sqrt{2^2 + 2^2} = \sqrt{8}$。
因此，以正方形$ABCD$的顶点$A$为起点（或网格中的其他合适点），向右水平移动$2$个单位，再向上垂直移动$2$个单位，到达点$G$。
连接$AG$（或相应的线段），则$AG$的长度为$\sqrt{8}$。
以原点为圆心，$AG$为半径画弧，与数轴正半轴的交点即为表示$\sqrt{8}$的点。
【答案】：（1）点$E$表示的数是$\sqrt{5}$；
（2）以$D$为起点，向右水平移动$1$个单位，再向上垂直移动$3$个单位，连接$DF$，以原点为圆心，$DF$为半径画弧，与数轴正半轴交点即为$\sqrt{10}$；
（3）以$A$（或其他合适点）为起点，向右水平移动$2$个单位，再向上垂直移动$2$个单位，连接$AG$（或相应的线段），以原点为圆心，$AG$为半径画弧，与数轴正半轴交点即为$\sqrt{8}$。