19. 阅读理解:
∵$1^2<2<2^2,$
∴1<√2<2,
即√2大于1,且√2小于2.
又∵$1.4^2= 1.96,1.5^2= 2.25,$
∴√2介于1.4与1.5之间.
1.4是√2的近似值,且它小于√2,称1.4为√2的不足近似值,1.4和√2的误差不超过0.1.
按照上面的方法,求:
(1)√3的不足近似值,且误差不超过0.1;
(2)√[3]{5}的不足近似值,且误差不超过0.1.
∵$1^2<2<2^2,$
∴1<√2<2,
即√2大于1,且√2小于2.
又∵$1.4^2= 1.96,1.5^2= 2.25,$
∴√2介于1.4与1.5之间.
1.4是√2的近似值,且它小于√2,称1.4为√2的不足近似值,1.4和√2的误差不超过0.1.
按照上面的方法,求:
(1)√3的不足近似值,且误差不超过0.1;
(2)√[3]{5}的不足近似值,且误差不超过0.1.
答案:【解析】:
本题主要考察平方根和立方数的近似计算以及如何通过比较来确定一个数的近似值。
(1) 对于$\sqrt{3}$,我们需要找到一个数,其平方接近但小于3,且与3的误差不超过0.1的平方。
(2) 对于$\sqrt[3]{5}$,我们需要找到一个数,其立方接近但小于5,且与5的误差不超过0.1的立方。
【答案】:
(1) 解:
首先,我们考虑$\sqrt{3}$的近似值。
由于$1^2 = 1 < 3$且$2^2 = 4 > 3$,我们知道$1 < \sqrt{3} < 2$。
进一步,我们计算$1.7^2 = 2.89 < 3$且$1.8^2 = 3.24 > 3$,
所以$\sqrt{3}$介于1.7与1.8之间。
由于$1.7$是$\sqrt{3}$的不足近似值,且误差不超过0.1(因为$1.8 - 1.7 = 0.1$),
所以$\sqrt{3}$的不足近似值为1.7。
(2) 解:
接着,我们考虑$\sqrt[3]{5}$的近似值。
由于$1^3 = 1 < 5$且$2^3 = 8 > 5$,我们知道$1 < \sqrt[3]{5} < 2$。
进一步计算,$1.7^3 = 4.913 < 5$且$1.8^3 = 5.832 > 5$,
所以$\sqrt[3]{5}$介于1.7与1.8之间。
由于$1.7$是$\sqrt[3]{5}$的不足近似值,且误差不超过0.1(因为$1.8 - 1.7 = 0.1$),
所以$\sqrt[3]{5}$的不足近似值为1.7。
本题主要考察平方根和立方数的近似计算以及如何通过比较来确定一个数的近似值。
(1) 对于$\sqrt{3}$,我们需要找到一个数,其平方接近但小于3,且与3的误差不超过0.1的平方。
(2) 对于$\sqrt[3]{5}$,我们需要找到一个数,其立方接近但小于5,且与5的误差不超过0.1的立方。
【答案】:
(1) 解:
首先,我们考虑$\sqrt{3}$的近似值。
由于$1^2 = 1 < 3$且$2^2 = 4 > 3$,我们知道$1 < \sqrt{3} < 2$。
进一步,我们计算$1.7^2 = 2.89 < 3$且$1.8^2 = 3.24 > 3$,
所以$\sqrt{3}$介于1.7与1.8之间。
由于$1.7$是$\sqrt{3}$的不足近似值,且误差不超过0.1(因为$1.8 - 1.7 = 0.1$),
所以$\sqrt{3}$的不足近似值为1.7。
(2) 解:
接着,我们考虑$\sqrt[3]{5}$的近似值。
由于$1^3 = 1 < 5$且$2^3 = 8 > 5$,我们知道$1 < \sqrt[3]{5} < 2$。
进一步计算,$1.7^3 = 4.913 < 5$且$1.8^3 = 5.832 > 5$,
所以$\sqrt[3]{5}$介于1.7与1.8之间。
由于$1.7$是$\sqrt[3]{5}$的不足近似值,且误差不超过0.1(因为$1.8 - 1.7 = 0.1$),
所以$\sqrt[3]{5}$的不足近似值为1.7。
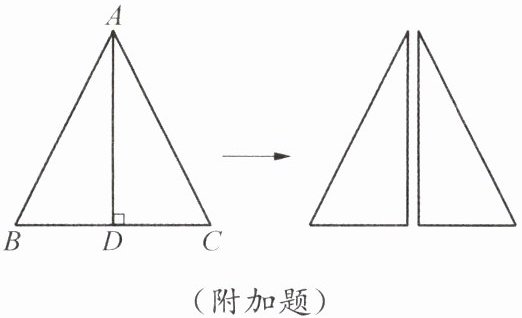
如图,在△ABC中,AB= AC,AD⊥BC,垂足为D,且AD= BC= 4.把△ABC沿AD剪开成两个三角形,在平面上把这两个三角形拼成一个四边形.你能拼出所有的不同形状的四边形吗?画出示意图,分别求出所拼四边形的对角线长.

答案:解:能拼出3种不同形状的四边形。
情况1:以AD为公共边拼接
示意图:两个直角三角形斜边AB、AC朝外,AD重合。
四边形为矩形,对角线长均为:$\sqrt{2^2 + 4^2} = 2\sqrt{5}$。
情况2:以BD为公共边拼接
示意图:将△ABD绕BD旋转180°,使A与C对应点重合。
四边形为平行四边形,对角线长分别为:AD=4,BC=4。
情况3:以AB为公共边拼接
示意图:将△ABD与△ACD沿AB反向拼接,使D与C对应点共线。
四边形为等腰梯形,对角线长为:$\sqrt{(4+2)^2 + 2^2} = 2\sqrt{10}$。
(注:示意图需根据描述自行绘制,此处省略图形。)
结论:三种四边形的对角线长分别为$2\sqrt{5}$、4和4、$2\sqrt{10}$。
情况1:以AD为公共边拼接
示意图:两个直角三角形斜边AB、AC朝外,AD重合。
四边形为矩形,对角线长均为:$\sqrt{2^2 + 4^2} = 2\sqrt{5}$。
情况2:以BD为公共边拼接
示意图:将△ABD绕BD旋转180°,使A与C对应点重合。
四边形为平行四边形,对角线长分别为:AD=4,BC=4。
情况3:以AB为公共边拼接
示意图:将△ABD与△ACD沿AB反向拼接,使D与C对应点共线。
四边形为等腰梯形,对角线长为:$\sqrt{(4+2)^2 + 2^2} = 2\sqrt{10}$。
(注:示意图需根据描述自行绘制,此处省略图形。)
结论:三种四边形的对角线长分别为$2\sqrt{5}$、4和4、$2\sqrt{10}$。