1. 直角边长分别为3和4的直角三角形的斜边长为
5
.答案:【解析】:
本题考查勾股定理的应用。在直角三角形中,已知两直角边长,求斜边长,可以直接使用勾股定理进行计算。勾股定理公式为$c=\sqrt{a^{2}+b^{2}}$,其中c是斜边长,a和b分别是两直角边长。
【答案】:
解:根据勾股定理,直角三角形的斜边长c满足$c=\sqrt{a^{2}+b^{2}}$。
将a=3,b=4代入公式,得
$c=\sqrt{3^{2}+4^{2}}=\sqrt{9+16}=\sqrt{25}=5$
所以,直角边长分别为3和4的直角三角形的斜边长为5。
本题考查勾股定理的应用。在直角三角形中,已知两直角边长,求斜边长,可以直接使用勾股定理进行计算。勾股定理公式为$c=\sqrt{a^{2}+b^{2}}$,其中c是斜边长,a和b分别是两直角边长。
【答案】:
解:根据勾股定理,直角三角形的斜边长c满足$c=\sqrt{a^{2}+b^{2}}$。
将a=3,b=4代入公式,得
$c=\sqrt{3^{2}+4^{2}}=\sqrt{9+16}=\sqrt{25}=5$
所以,直角边长分别为3和4的直角三角形的斜边长为5。
2. 已知等腰三角形中相等的两边长为10 cm,第三边长为16 cm,则底边上的高为
6
cm.答案:【解析】:
本题主要考查等腰三角形的性质以及勾股定理的应用。
首先,根据等腰三角形的性质,我们知道等腰三角形的两腰相等,这里相等的两边长为$10 cm$,底边长为$16 cm$。
设等腰三角形为$\triangle ABC$,其中$AB = AC = 10 cm$,$BC = 16 cm$。
作$AD \perp BC$于点$D$,则$AD$就是底边上的高。
由于$\triangle ABC$是等腰三角形,根据等腰三角形的性质,$D$是$BC$的中点,所以$BD = \frac{BC}{2} = 8 cm$。
接下来,我们利用勾股定理来求$AD$的长度。
勾股定理公式为:$a^2 + b^2 = c^2$,其中$c$是斜边,$a$和$b$是直角边。
在直角三角形$\triangle ABD$中,$AB$是斜边,$BD$和$AD$是直角边。
所以,我们有:
$AD = \sqrt{AB^2 - BD^2}$
$= \sqrt{10^2 - 8^2}$
$= \sqrt{100 - 64}$
$= \sqrt{36}$
$= 6 cm$
【答案】:
$6$
本题主要考查等腰三角形的性质以及勾股定理的应用。
首先,根据等腰三角形的性质,我们知道等腰三角形的两腰相等,这里相等的两边长为$10 cm$,底边长为$16 cm$。
设等腰三角形为$\triangle ABC$,其中$AB = AC = 10 cm$,$BC = 16 cm$。
作$AD \perp BC$于点$D$,则$AD$就是底边上的高。
由于$\triangle ABC$是等腰三角形,根据等腰三角形的性质,$D$是$BC$的中点,所以$BD = \frac{BC}{2} = 8 cm$。
接下来,我们利用勾股定理来求$AD$的长度。
勾股定理公式为:$a^2 + b^2 = c^2$,其中$c$是斜边,$a$和$b$是直角边。
在直角三角形$\triangle ABD$中,$AB$是斜边,$BD$和$AD$是直角边。
所以,我们有:
$AD = \sqrt{AB^2 - BD^2}$
$= \sqrt{10^2 - 8^2}$
$= \sqrt{100 - 64}$
$= \sqrt{36}$
$= 6 cm$
【答案】:
$6$
3. 如图,所有四边形都是正方形,所有三角形都是直角三角形.其中,最大的正方形的边长为7,则正方形A,B,C,D的面积之和为
49
.答案:解:设正方形A、B、C、D的边长分别为a、b、c、d,面积分别为Sₐ、Sᵦ、Sₑ、Sᵈ。
由勾股定理,以A、B为边的两个正方形所对直角三角形的斜边长的平方为a²+b²,即Sₐ+Sᵦ;同理,以C、D为边的两个正方形所对直角三角形的斜边长的平方为c²+d²,即Sₑ+Sᵈ。
最大正方形边长为7,其面积为7²=49,该面积等于上述两个斜边长的平方之和,即(Sₐ+Sᵦ)+(Sₑ+Sᵈ)=49。
故正方形A、B、C、D的面积之和为49。
答案:49
由勾股定理,以A、B为边的两个正方形所对直角三角形的斜边长的平方为a²+b²,即Sₐ+Sᵦ;同理,以C、D为边的两个正方形所对直角三角形的斜边长的平方为c²+d²,即Sₑ+Sᵈ。
最大正方形边长为7,其面积为7²=49,该面积等于上述两个斜边长的平方之和,即(Sₐ+Sᵦ)+(Sₑ+Sᵈ)=49。
故正方形A、B、C、D的面积之和为49。
答案:49
4. 边长分别为6,8,10的三角形的形状是
直角三角形
.答案:解:因为$6^2 + 8^2 = 36 + 64 = 100$,$10^2 = 100$,所以$6^2 + 8^2 = 10^2$。根据勾股定理的逆定理,该三角形是直角三角形。
直角三角形
直角三角形
5. 如图,长方体的长、宽、高分别为4,3,12,则$BD_{1}= $
13
.答案:解:在长方体中,连接BD。
在Rt△ABD中,AD=4,AB=3,
由勾股定理得:BD²=AD²+AB²=4²+3²=16+9=25,
则BD=5。
在Rt△BDD₁中,DD₁=12,BD=5,
由勾股定理得:BD₁²=BD²+DD₁²=5²+12²=25+144=169,
则BD₁=13。
13
在Rt△ABD中,AD=4,AB=3,
由勾股定理得:BD²=AD²+AB²=4²+3²=16+9=25,
则BD=5。
在Rt△BDD₁中,DD₁=12,BD=5,
由勾股定理得:BD₁²=BD²+DD₁²=5²+12²=25+144=169,
则BD₁=13。
13
6. 直角三角形的一条直角边长为11,另两条边均为自然数,则其周长为______
132
.答案:解:设另一条直角边为$a$,斜边为$c$($a$、$c$为自然数,且$c > a$)。
由勾股定理得:$a^2 + 11^2 = c^2$,即$c^2 - a^2 = 121$。
因式分解得:$(c - a)(c + a) = 121$。
因为$121 = 1×121$,且$c - a$、$c + a$为正整数,$c - a < c + a$,
所以$\begin{cases}c - a = 1 \\ c + a = 121\end{cases}$
解得$\begin{cases}a = 60 \\ c = 61\end{cases}$
周长为$11 + 60 + 61 = 132$。
132
由勾股定理得:$a^2 + 11^2 = c^2$,即$c^2 - a^2 = 121$。
因式分解得:$(c - a)(c + a) = 121$。
因为$121 = 1×121$,且$c - a$、$c + a$为正整数,$c - a < c + a$,
所以$\begin{cases}c - a = 1 \\ c + a = 121\end{cases}$
解得$\begin{cases}a = 60 \\ c = 61\end{cases}$
周长为$11 + 60 + 61 = 132$。
132
7. 如果梯子的底端离建筑物9 m,那么15 m长的梯子的顶端到达建筑物的高度是
12
m.答案:【解析】:
本题主要考察勾股定理的应用。在直角三角形中,已知直角边和斜边的长度,求另一直角边的长度。
设梯子顶端到达建筑物的高度为$x$米,梯子的长度为15米,梯子底端离建筑物的距离为9米。
根据勾股定理,有:
$x^2 + 9^2 = 15^2$,
$x^2 = 15^2 - 9^2$,
$x^2 = 225 - 81$,
$x^2 = 144$,
解得 $x = 12$ (负值舍去,因为高度不能为负)。
【答案】:
12。
本题主要考察勾股定理的应用。在直角三角形中,已知直角边和斜边的长度,求另一直角边的长度。
设梯子顶端到达建筑物的高度为$x$米,梯子的长度为15米,梯子底端离建筑物的距离为9米。
根据勾股定理,有:
$x^2 + 9^2 = 15^2$,
$x^2 = 15^2 - 9^2$,
$x^2 = 225 - 81$,
$x^2 = 144$,
解得 $x = 12$ (负值舍去,因为高度不能为负)。
【答案】:
12。
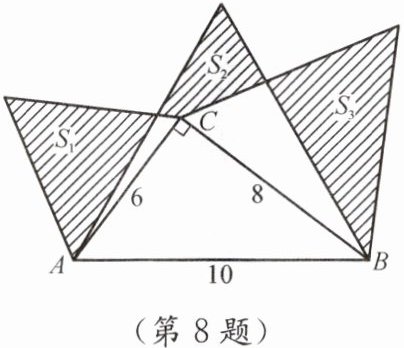
8. 如图,分别以Rt△ABC的三边作正三角形,已知$AC= 6$,$AB= 10$,阴影部分的面积分别记为$S_{1},S_{2},S_{3}$,则$S_{1}+S_{3}-S_{2}$的值为______.

0
答案:解:在Rt△ABC中,∠C=90°,AC=6,AB=10,
由勾股定理得BC=$\sqrt{A{B}^{2}-A{C}^{2}}=\sqrt{1{0}^{2}-{6}^{2}}=8$。
设以AC、BC、AB为边的正三角形面积分别为Sₐ、Sᵦ、Sₙ。
正三角形面积公式为$S=\frac{\sqrt{3}}{4}a^{2}$(a为边长),
则$S_{a}=\frac{\sqrt{3}}{4}×6^{2}=9\sqrt{3}$,
$S_{b}=\frac{\sqrt{3}}{4}×8^{2}=16\sqrt{3}$,
$S_{c}=\frac{\sqrt{3}}{4}×10^{2}=25\sqrt{3}$。
由图形可知$S_{1}+S_{3}=S_{a}+S_{b}$,$S_{2}=S_{c}-(空白部分)$,但空白部分为$S_{a}+S_{b}-S_{1}-S_{3}$,
故$S_{1}+S_{3}-S_{2}=S_{a}+S_{b}-(S_{c}-(S_{a}+S_{b}-S_{1}-S_{3}))$,化简后得$S_{a}+S_{b}-S_{c}$。
所以$S_{1}+S_{3}-S_{2}=9\sqrt{3}+16\sqrt{3}-25\sqrt{3}=0$。
0
由勾股定理得BC=$\sqrt{A{B}^{2}-A{C}^{2}}=\sqrt{1{0}^{2}-{6}^{2}}=8$。
设以AC、BC、AB为边的正三角形面积分别为Sₐ、Sᵦ、Sₙ。
正三角形面积公式为$S=\frac{\sqrt{3}}{4}a^{2}$(a为边长),
则$S_{a}=\frac{\sqrt{3}}{4}×6^{2}=9\sqrt{3}$,
$S_{b}=\frac{\sqrt{3}}{4}×8^{2}=16\sqrt{3}$,
$S_{c}=\frac{\sqrt{3}}{4}×10^{2}=25\sqrt{3}$。
由图形可知$S_{1}+S_{3}=S_{a}+S_{b}$,$S_{2}=S_{c}-(空白部分)$,但空白部分为$S_{a}+S_{b}-S_{1}-S_{3}$,
故$S_{1}+S_{3}-S_{2}=S_{a}+S_{b}-(S_{c}-(S_{a}+S_{b}-S_{1}-S_{3}))$,化简后得$S_{a}+S_{b}-S_{c}$。
所以$S_{1}+S_{3}-S_{2}=9\sqrt{3}+16\sqrt{3}-25\sqrt{3}=0$。
0
9. 已知一个直角三角形的两边长分别为3,4,则第三边的平方是(
A.25
B.5
C.7
D.7或25
D
).A.25
B.5
C.7
D.7或25
答案:解:情况一:当3,4为直角边时,第三边平方为$3^{2}+4^{2}=9 + 16=25$。
情况二:当4为斜边,3为直角边时,第三边平方为$4^{2}-3^{2}=16 - 9=7$。
结论:第三边的平方是7或25。
答案:D
情况二:当4为斜边,3为直角边时,第三边平方为$4^{2}-3^{2}=16 - 9=7$。
结论:第三边的平方是7或25。
答案:D
10. 在△ABC中,∠A,∠B,∠C的度数之比为1:2:3,则对应边a,b,c的关系为(
A.$a:b:c= 3:4:5$
B.$3a= 2b= c$
C.$a^{2}+b^{2}= c^{2}$
D.$a:b:c= 4:5:6$
C
).A.$a:b:c= 3:4:5$
B.$3a= 2b= c$
C.$a^{2}+b^{2}= c^{2}$
D.$a:b:c= 4:5:6$
答案:【解析】:
本题考察的是三角形内角的关系以及勾股定理的应用。
首先根据题目条件,三角形ABC的三个内角的度数之比为1:2:3,而三角形的内角和为180度,由此可以计算出每个角的度数。
步骤一:计算三角形ABC的每个角的度数
$\angle A = 180^\circ × \frac{1}{1+2+3} = 30^\circ$
$\angle B = 180^\circ × \frac{2}{1+2+3} = 60^\circ$
$\angle C = 180^\circ × \frac{3}{1+2+3} = 90^\circ$
步骤二:判断三角形的类型
由于$\angle C = 90^\circ$,所以$\bigtriangleup ABC$是直角三角形。
步骤三:应用勾股定理
在直角三角形中,根据勾股定理,有$a^2 + b^2 = c^2$。
【答案】:C.$a^{2}+b^{2}= c^{2}$
本题考察的是三角形内角的关系以及勾股定理的应用。
首先根据题目条件,三角形ABC的三个内角的度数之比为1:2:3,而三角形的内角和为180度,由此可以计算出每个角的度数。
步骤一:计算三角形ABC的每个角的度数
$\angle A = 180^\circ × \frac{1}{1+2+3} = 30^\circ$
$\angle B = 180^\circ × \frac{2}{1+2+3} = 60^\circ$
$\angle C = 180^\circ × \frac{3}{1+2+3} = 90^\circ$
步骤二:判断三角形的类型
由于$\angle C = 90^\circ$,所以$\bigtriangleup ABC$是直角三角形。
步骤三:应用勾股定理
在直角三角形中,根据勾股定理,有$a^2 + b^2 = c^2$。
【答案】:C.$a^{2}+b^{2}= c^{2}$