11. 在锐角三角形ABC中,三边a,b,c(c为最大边)的关系为(
A.$a^{2}+b^{2}>c^{2}$
B.$a^{2}+b^{2}= c^{2}$
C.$a^{2}+b^{2}<c^{2}$
D.$a^{2}+b^{2}= ac+bc$
A
).A.$a^{2}+b^{2}>c^{2}$
B.$a^{2}+b^{2}= c^{2}$
C.$a^{2}+b^{2}<c^{2}$
D.$a^{2}+b^{2}= ac+bc$
答案:【解析】:
本题主要考查勾股定理以及三角形的性质。
在直角三角形中,如果$c$为斜边,那么有$a^{2} + b^{2} = c^{2}$。但在锐角三角形中,由于所有的角都小于$90^\circ$,因此当$c$为最大边时,其对应的角必然小于$90^\circ$。根据余弦定理,我们有$\cos C = \frac{a^{2} + b^{2} - c^{2}}{2ab}$。由于$C < 90^\circ$,所以$\cos C > 0$,从而得出$a^{2} + b^{2} > c^{2}$。
接下来,我们逐一排除选项:
B选项$a^{2} + b^{2} = c^{2}$,这是直角三角形的性质,与题目中的锐角三角形矛盾,所以B选项错误。
C选项$a^{2} + b^{2} < c^{2}$,这通常表示$c$边对应的角大于$90^\circ$,与题目中的锐角三角形矛盾,所以C选项错误。
D选项$a^{2} + b^{2} = ac + bc$,这个等式无法直接由三角形的性质得出,且与勾股定理或余弦定理无直接关联,所以D选项错误。
因此,通过排除法以及利用余弦定理的理解,我们可以确定A选项$a^{2} + b^{2} > c^{2}$是正确的。
【答案】:
A.$a^{2}+b^{2}>c^{2}$
本题主要考查勾股定理以及三角形的性质。
在直角三角形中,如果$c$为斜边,那么有$a^{2} + b^{2} = c^{2}$。但在锐角三角形中,由于所有的角都小于$90^\circ$,因此当$c$为最大边时,其对应的角必然小于$90^\circ$。根据余弦定理,我们有$\cos C = \frac{a^{2} + b^{2} - c^{2}}{2ab}$。由于$C < 90^\circ$,所以$\cos C > 0$,从而得出$a^{2} + b^{2} > c^{2}$。
接下来,我们逐一排除选项:
B选项$a^{2} + b^{2} = c^{2}$,这是直角三角形的性质,与题目中的锐角三角形矛盾,所以B选项错误。
C选项$a^{2} + b^{2} < c^{2}$,这通常表示$c$边对应的角大于$90^\circ$,与题目中的锐角三角形矛盾,所以C选项错误。
D选项$a^{2} + b^{2} = ac + bc$,这个等式无法直接由三角形的性质得出,且与勾股定理或余弦定理无直接关联,所以D选项错误。
因此,通过排除法以及利用余弦定理的理解,我们可以确定A选项$a^{2} + b^{2} > c^{2}$是正确的。
【答案】:
A.$a^{2}+b^{2}>c^{2}$
12. 直角三角形的两条直角边分别为a,b,斜边上的高为h,下列各式中,正确的是(
A.$ab= h^{2}$
B.$a^{2}+b^{2}= h^{2}$
C.$\frac{1}{a}+\frac{1}{b}= \frac{1}{h}$
D.$\frac{1}{a^{2}}+\frac{1}{b^{2}}= \frac{1}{h^{2}}$
D
).A.$ab= h^{2}$
B.$a^{2}+b^{2}= h^{2}$
C.$\frac{1}{a}+\frac{1}{b}= \frac{1}{h}$
D.$\frac{1}{a^{2}}+\frac{1}{b^{2}}= \frac{1}{h^{2}}$
答案:解:设直角三角形斜边为c。
由勾股定理得:$a^{2}+b^{2}=c^{2}$。
三角形面积$S=\frac{1}{2}ab=\frac{1}{2}ch$,则$ab=ch$,$c=\frac{ab}{h}$。
将$c=\frac{ab}{h}$代入$a^{2}+b^{2}=c^{2}$,得$a^{2}+b^{2}=(\frac{ab}{h})^{2}$。
等式两边同除以$a^{2}b^{2}$:$\frac{a^{2}}{a^{2}b^{2}}+\frac{b^{2}}{a^{2}b^{2}}=\frac{a^{2}b^{2}}{h^{2}a^{2}b^{2}}$,即$\frac{1}{b^{2}}+\frac{1}{a^{2}}=\frac{1}{h^{2}}$。
答案:D
由勾股定理得:$a^{2}+b^{2}=c^{2}$。
三角形面积$S=\frac{1}{2}ab=\frac{1}{2}ch$,则$ab=ch$,$c=\frac{ab}{h}$。
将$c=\frac{ab}{h}$代入$a^{2}+b^{2}=c^{2}$,得$a^{2}+b^{2}=(\frac{ab}{h})^{2}$。
等式两边同除以$a^{2}b^{2}$:$\frac{a^{2}}{a^{2}b^{2}}+\frac{b^{2}}{a^{2}b^{2}}=\frac{a^{2}b^{2}}{h^{2}a^{2}b^{2}}$,即$\frac{1}{b^{2}}+\frac{1}{a^{2}}=\frac{1}{h^{2}}$。
答案:D
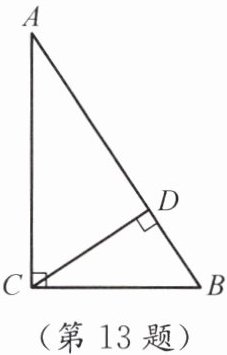
13. 如图,在Rt△ABC中,$\angle ACB= 90^{\circ}$.
(1)已知$BC= 5$,$AB= 13$,求AC;
(2)若斜边AB上的高为CD,求CD.
(1)已知$BC= 5$,$AB= 13$,求AC;
(2)若斜边AB上的高为CD,求CD.

答案:【解析】:
本题主要考查勾股定理以及三角形面积的计算。
(1) 在$Rt \bigtriangleup ABC$中,已知$BC = 5$,$AB = 13$,$\angle ACB = 90^{\circ}$。
根据勾股定理$AB^{2}=AC^{2}+BC^{2}$,可得$AC = \sqrt{AB^{2}-BC^{2}}$。
将$BC = 5$,$AB = 13$代入上式,即$AC=\sqrt{13^{2} - 5^{2}}=\sqrt{169 - 25}=\sqrt{144}=12$。
(2) 已知在$Rt \bigtriangleup ABC$中,$BC = 5$,$AC = 12$,$AB = 13$。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),对于$Rt \bigtriangleup ABC$,以$AC$、$BC$为直角边时,面积$S_{\bigtriangleup ABC}=\frac{1}{2}AC\cdot BC$;以$AB$为底,$CD$为高时,面积$S_{\bigtriangleup ABC}=\frac{1}{2}AB\cdot CD$。
因为三角形面积是固定的,所以$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$,则$CD = \frac{AC\cdot BC}{AB}$。
把$AC = 12$,$BC = 5$,$AB = 13$代入可得$CD=\frac{12×5}{13}=\frac{60}{13}$。
【答案】:
(1)$AC = 12$;
(2)$CD=\frac{60}{13}$。
本题主要考查勾股定理以及三角形面积的计算。
(1) 在$Rt \bigtriangleup ABC$中,已知$BC = 5$,$AB = 13$,$\angle ACB = 90^{\circ}$。
根据勾股定理$AB^{2}=AC^{2}+BC^{2}$,可得$AC = \sqrt{AB^{2}-BC^{2}}$。
将$BC = 5$,$AB = 13$代入上式,即$AC=\sqrt{13^{2} - 5^{2}}=\sqrt{169 - 25}=\sqrt{144}=12$。
(2) 已知在$Rt \bigtriangleup ABC$中,$BC = 5$,$AC = 12$,$AB = 13$。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),对于$Rt \bigtriangleup ABC$,以$AC$、$BC$为直角边时,面积$S_{\bigtriangleup ABC}=\frac{1}{2}AC\cdot BC$;以$AB$为底,$CD$为高时,面积$S_{\bigtriangleup ABC}=\frac{1}{2}AB\cdot CD$。
因为三角形面积是固定的,所以$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$,则$CD = \frac{AC\cdot BC}{AB}$。
把$AC = 12$,$BC = 5$,$AB = 13$代入可得$CD=\frac{12×5}{13}=\frac{60}{13}$。
【答案】:
(1)$AC = 12$;
(2)$CD=\frac{60}{13}$。
14. 《九章算术》勾股章中有一题:“今有两人同立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙相会.问甲乙行各几何?”大意是:已知甲、乙二人同时从同一地点出发,甲的速度为7,乙的速度为3,乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇,甲、乙各走了多少步?请你解答这个问题.
答案:解:设甲、乙相遇时,乙走了$3x$步,甲共走了$7x$步。
甲先向南走10步,则斜向北偏东方向走了$(7x - 10)$步。
乙向东走的距离为$3x$步,甲向南走的10步与乙向东走的$3x$步及甲斜走的$(7x - 10)$步构成直角三角形,其中甲斜走的距离为斜边。
根据勾股定理可得:$10^2 + (3x)^2 = (7x - 10)^2$
展开得:$100 + 9x^2 = 49x^2 - 140x + 100$
移项化简得:$40x^2 - 140x = 0$
即:$10x(4x - 14) = 0$
解得:$x_1 = 0$(舍去),$x_2 = 3.5$
所以甲走的步数为:$7x = 7×3.5 = 24.5$(步)
乙走的步数为:$3x = 3×3.5 = 10.5$(步)
答:甲走了24.5步,乙走了10.5步。
甲先向南走10步,则斜向北偏东方向走了$(7x - 10)$步。
乙向东走的距离为$3x$步,甲向南走的10步与乙向东走的$3x$步及甲斜走的$(7x - 10)$步构成直角三角形,其中甲斜走的距离为斜边。
根据勾股定理可得:$10^2 + (3x)^2 = (7x - 10)^2$
展开得:$100 + 9x^2 = 49x^2 - 140x + 100$
移项化简得:$40x^2 - 140x = 0$
即:$10x(4x - 14) = 0$
解得:$x_1 = 0$(舍去),$x_2 = 3.5$
所以甲走的步数为:$7x = 7×3.5 = 24.5$(步)
乙走的步数为:$3x = 3×3.5 = 10.5$(步)
答:甲走了24.5步,乙走了10.5步。
15. 在△ABC中,$AB= 20$,$AC= 13$,高$AD= 12$,求△ABC的面积.
答案:解:情况一:高AD在△ABC内部
在Rt△ABD中,BD=$\sqrt{AB^{2}-AD^{2}}=\sqrt{20^{2}-12^{2}}=16$
在Rt△ACD中,CD=$\sqrt{AC^{2}-AD^{2}}=\sqrt{13^{2}-12^{2}}=5$
BC=BD+CD=16+5=21
S_{△ABC}=$\frac{1}{2}×BC×AD=\frac{1}{2}×21×12=126$
情况二:高AD在△ABC外部
在Rt△ABD中,BD=$\sqrt{AB^{2}-AD^{2}}=\sqrt{20^{2}-12^{2}}=16$
在Rt△ACD中,CD=$\sqrt{AC^{2}-AD^{2}}=\sqrt{13^{2}-12^{2}}=5$
BC=BD-CD=16-5=11
S_{△ABC}=$\frac{1}{2}×BC×AD=\frac{1}{2}×11×12=66$
综上,△ABC的面积为126或66。
在Rt△ABD中,BD=$\sqrt{AB^{2}-AD^{2}}=\sqrt{20^{2}-12^{2}}=16$
在Rt△ACD中,CD=$\sqrt{AC^{2}-AD^{2}}=\sqrt{13^{2}-12^{2}}=5$
BC=BD+CD=16+5=21
S_{△ABC}=$\frac{1}{2}×BC×AD=\frac{1}{2}×21×12=126$
情况二:高AD在△ABC外部
在Rt△ABD中,BD=$\sqrt{AB^{2}-AD^{2}}=\sqrt{20^{2}-12^{2}}=16$
在Rt△ACD中,CD=$\sqrt{AC^{2}-AD^{2}}=\sqrt{13^{2}-12^{2}}=5$
BC=BD-CD=16-5=11
S_{△ABC}=$\frac{1}{2}×BC×AD=\frac{1}{2}×11×12=66$
综上,△ABC的面积为126或66。