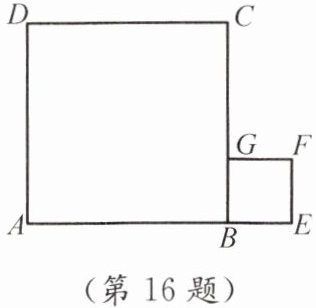
16. 如图,点A,B,E在一条直线上,且四边形ABCD和四边形BEFG都是正方形.在图中画一个正方形,使所画的正方形的面积等于正方形ABCD与正方形BEFG的面积之和(直接画出图形即可).

答案:【解析】:本题可根据勾股定理以及正方形的面积公式来构造满足条件的正方形。
设正方形$ABCD$的边长为$a$,正方形$BEFG$的边长为$b$。
根据正方形面积公式$S = 边长×边长$,可得正方形$ABCD$的面积$S_{ABCD}=a^{2}$,正方形$BEFG$的面积$S_{BEFG}=b^{2}$。
那么两个正方形面积之和为$S = S_{ABCD}+S_{BEFG}=a^{2}+b^{2}$。
连接$AG$,在$Rt\triangle ABG$中,$AB = a$,$BG = b$,根据勾股定理$AG^{2}=AB^{2}+BG^{2}=a^{2}+b^{2}$。
所以以$AG$为边长作正方形,其面积就等于正方形$ABCD$与正方形$BEFG$的面积之和。
【答案】:图略(以$AG$为边长作正方形即可)。
设正方形$ABCD$的边长为$a$,正方形$BEFG$的边长为$b$。
根据正方形面积公式$S = 边长×边长$,可得正方形$ABCD$的面积$S_{ABCD}=a^{2}$,正方形$BEFG$的面积$S_{BEFG}=b^{2}$。
那么两个正方形面积之和为$S = S_{ABCD}+S_{BEFG}=a^{2}+b^{2}$。
连接$AG$,在$Rt\triangle ABG$中,$AB = a$,$BG = b$,根据勾股定理$AG^{2}=AB^{2}+BG^{2}=a^{2}+b^{2}$。
所以以$AG$为边长作正方形,其面积就等于正方形$ABCD$与正方形$BEFG$的面积之和。
【答案】:图略(以$AG$为边长作正方形即可)。
17. 利用如图所示的图形证明勾股定理:
如图,在四边形ABCD中,$BD\perp CD$,$AE\perp BD$,垂足分别为D,E,且△ABE≌△BCD.
求证:$AB^{2}= BE^{2}+AE^{2}$.

如图,在四边形ABCD中,$BD\perp CD$,$AE\perp BD$,垂足分别为D,E,且△ABE≌△BCD.
求证:$AB^{2}= BE^{2}+AE^{2}$.

答案:【解析】:本题主要考查勾股定理的证明,利用三角形全等的性质来推导。
已知$\triangle ABE\cong\triangle BCD$,根据全等三角形的性质可知,对应边相等,对应角相等。
所以$AB = BC$,$AE = BD$,$BE = CD$,$\angle BAE=\angle CBD$。
因为$BD\perp CD$,$AE\perp BD$,所以$\angle BDC = \angle AEB = 90^{\circ}$。
在$Rt\triangle ABE$中,根据勾股定理,直角三角形的两条直角边的平方和等于斜边的平方,可得$AB^{2}=BE^{2}+AE^{2}$。
【答案】:证明:
∵$\triangle ABE\cong\triangle BCD$,
∴$AB = BC$,$AE = BD$,$BE = CD$,$\angle BAE=\angle CBD$。
∵$BD\perp CD$,$AE\perp BD$,
∴$\angle BDC = \angle AEB = 90^{\circ}$。
在$Rt\triangle ABE$中,
∴$AB^{2}=BE^{2}+AE^{2}$。
已知$\triangle ABE\cong\triangle BCD$,根据全等三角形的性质可知,对应边相等,对应角相等。
所以$AB = BC$,$AE = BD$,$BE = CD$,$\angle BAE=\angle CBD$。
因为$BD\perp CD$,$AE\perp BD$,所以$\angle BDC = \angle AEB = 90^{\circ}$。
在$Rt\triangle ABE$中,根据勾股定理,直角三角形的两条直角边的平方和等于斜边的平方,可得$AB^{2}=BE^{2}+AE^{2}$。
【答案】:证明:
∵$\triangle ABE\cong\triangle BCD$,
∴$AB = BC$,$AE = BD$,$BE = CD$,$\angle BAE=\angle CBD$。
∵$BD\perp CD$,$AE\perp BD$,
∴$\angle BDC = \angle AEB = 90^{\circ}$。
在$Rt\triangle ABE$中,
∴$AB^{2}=BE^{2}+AE^{2}$。
18. 在一次探究性学习课中,老师设计了下表.

(1)观察表格,根据规律在表中填空.
(2)用含自然数n($n>1$)的代数式表示a,b,c,则a=
(3)猜想:以a,b,c为边的三角形是否为直角三角形?证明你的结论.
以a,b,c为边的三角形是直角三角形,证明如下:
因为$a^2 + b^2 = (n^2 - 1)^2 + (2n)^2 = n^4 - 2n^2 + 1 + 4n^2 = n^4 + 2n^2 + 1$,$c^2 = (n^2 + 1)^2 = n^4 + 2n^2 + 1$,所以$a^2 + b^2 = c^2$,故以a,b,c为边的三角形是直角三角形。

(1)观察表格,根据规律在表中填空.
24
12
37
(2)用含自然数n($n>1$)的代数式表示a,b,c,则a=
$n^2 - 1$
,b=$2n$
,c=$n^2 + 1$
.(3)猜想:以a,b,c为边的三角形是否为直角三角形?证明你的结论.
以a,b,c为边的三角形是直角三角形,证明如下:
因为$a^2 + b^2 = (n^2 - 1)^2 + (2n)^2 = n^4 - 2n^2 + 1 + 4n^2 = n^4 + 2n^2 + 1$,$c^2 = (n^2 + 1)^2 = n^4 + 2n^2 + 1$,所以$a^2 + b^2 = c^2$,故以a,b,c为边的三角形是直角三角形。
答案:【解析】:
(1)观察表格,可以看到当$n=2$时,$a=2^2 - 1$,$b=4=2 × 2$,$c=2^2 + 1$;
当$n=3$时,$a=3^2 - 1$,$b=6=2 × 3$,$c=3^2 + 1$;
当$n=4$时,$a=4^2 - 1$,$b=8=2 × 4$,$c=4^2 + 1$;
依此类推,当$n=6$时,$a=6^2 - 1 = 35$,$b=2 × 6 = 12$,$c=6^2 + 1 = 37$;
所以当$n=5$时,$a=5^2 - 1 = 24$,$b=2 × 5 = 12 × 2 ÷ 2 = 10 × 2 ÷ (2 ÷ 1) = 2 × 5 = 10$(这里直接$2 × 5=10$即可,前面是冗余的计算过程,直接$b=2n$当$n=5$时就是$10$),$c=5^2 + 1 = 26$;
本题应填:24;12;37。
(2)根据上述规律,可以得出:
$a = n^2 - 1$,
$b = 2n$,
$c = n^2 + 1$;
本题答案为$n^2 - 1$;$2n$;$n^2 + 1$。
(3)为了证明以$a,b,c$为边的三角形是否为直角三角形,需要验证是否满足勾股定理,即$a^2 + b^2 = c^2$。
根据
(2)中得出的代数式,有:
$a^2 + b^2 = (n^2 - 1)^2 + (2n)^2$
$= n^4 - 2n^2 + 1 + 4n^2$
$= n^4 + 2n^2 + 1$
$c^2 = (n^2 + 1)^2$
$= n^4 + 2n^2 + 1$
由此可见$a^2 + b^2 = c^2$,
所以以$a,b,c$为边的三角形是直角三角形。
【答案】:
(1) $24$;$12$;$37$
(2) $n^2 - 1$;$2n$;$n^2 + 1$
(3) 以$a,b,c$为边的三角形是直角三角形,证明见上述解析过程。
(1)观察表格,可以看到当$n=2$时,$a=2^2 - 1$,$b=4=2 × 2$,$c=2^2 + 1$;
当$n=3$时,$a=3^2 - 1$,$b=6=2 × 3$,$c=3^2 + 1$;
当$n=4$时,$a=4^2 - 1$,$b=8=2 × 4$,$c=4^2 + 1$;
依此类推,当$n=6$时,$a=6^2 - 1 = 35$,$b=2 × 6 = 12$,$c=6^2 + 1 = 37$;
所以当$n=5$时,$a=5^2 - 1 = 24$,$b=2 × 5 = 12 × 2 ÷ 2 = 10 × 2 ÷ (2 ÷ 1) = 2 × 5 = 10$(这里直接$2 × 5=10$即可,前面是冗余的计算过程,直接$b=2n$当$n=5$时就是$10$),$c=5^2 + 1 = 26$;
本题应填:24;12;37。
(2)根据上述规律,可以得出:
$a = n^2 - 1$,
$b = 2n$,
$c = n^2 + 1$;
本题答案为$n^2 - 1$;$2n$;$n^2 + 1$。
(3)为了证明以$a,b,c$为边的三角形是否为直角三角形,需要验证是否满足勾股定理,即$a^2 + b^2 = c^2$。
根据
(2)中得出的代数式,有:
$a^2 + b^2 = (n^2 - 1)^2 + (2n)^2$
$= n^4 - 2n^2 + 1 + 4n^2$
$= n^4 + 2n^2 + 1$
$c^2 = (n^2 + 1)^2$
$= n^4 + 2n^2 + 1$
由此可见$a^2 + b^2 = c^2$,
所以以$a,b,c$为边的三角形是直角三角形。
【答案】:
(1) $24$;$12$;$37$
(2) $n^2 - 1$;$2n$;$n^2 + 1$
(3) 以$a,b,c$为边的三角形是直角三角形,证明见上述解析过程。