1. 已知点P(2,-1)关于x轴的对称点是$P_1,$那么$P_1$点关于原点的对称点的坐标为
(-2,-1)
.答案:解:点P(2,-1)关于x轴的对称点P₁的坐标为(2,1)。
P₁(2,1)关于原点的对称点的坐标为(-2,-1)。
故答案为:(-2,-1)
P₁(2,1)关于原点的对称点的坐标为(-2,-1)。
故答案为:(-2,-1)
2. 在平面直角坐标系中,已知点A(-3,0),B(0,2).现将线段AB向右平移,使点A与坐标原点重合,则点B平移后的坐标是
(3,2)
.答案:解:线段AB向右平移,点A(-3,0)平移后与原点(0,0)重合,
平移规律为:向右平移3个单位长度(横坐标加3,纵坐标不变)。
点B(0,2)平移后的坐标为(0+3,2),即(3,2)。
答案:(3,2)
平移规律为:向右平移3个单位长度(横坐标加3,纵坐标不变)。
点B(0,2)平移后的坐标为(0+3,2),即(3,2)。
答案:(3,2)
3. 已知点O(0,0),B(1,2),点A在坐标轴上,且S△OAB= 2,则满足条件的点A的坐标为
(2,0),(-2,0),(0,4),(0,-4)
.答案:【解析】:
本题主要考查三角形面积的计算和坐标的确定。
由于点A在坐标轴上,所以A的坐标形式应为$(x,0)$或$(0,y)$。
当A在x轴上时,设A的坐标为$(x,0)$,此时三角形$OAB$的底为$OA$,高为$OB$的纵坐标的绝对值,即2。
根据三角形面积公式$S = \frac{1}{2} × 底 × 高$,我们有$S_{\bigtriangleup OAB} = \frac{1}{2} × |x| × 2 = 2$,
解得$x = \pm 2$,
所以A的坐标可能为$(2,0)$或$(-2,0)$。
当A在y轴上时,设A的坐标为$(0,y)$,此时三角形$OAB$的底为$OB$的横坐标的绝对值,即1,高为$|y|$。
同样根据三角形面积公式,我们有$S_{\bigtriangleup OAB} = \frac{1}{2} × 1 × |y| = 2$,
解得$y = \pm 4$,
所以A的坐标可能为$(0,4)$或$(0,-4)$。
综上,满足条件的点A的坐标为$(2,0)$,$(-2,0)$,$(0,4)$,$(0,-4)$。
【答案】:
$(2,0)$,$(-2,0)$,$(0,4)$,$(0,-4)$。
本题主要考查三角形面积的计算和坐标的确定。
由于点A在坐标轴上,所以A的坐标形式应为$(x,0)$或$(0,y)$。
当A在x轴上时,设A的坐标为$(x,0)$,此时三角形$OAB$的底为$OA$,高为$OB$的纵坐标的绝对值,即2。
根据三角形面积公式$S = \frac{1}{2} × 底 × 高$,我们有$S_{\bigtriangleup OAB} = \frac{1}{2} × |x| × 2 = 2$,
解得$x = \pm 2$,
所以A的坐标可能为$(2,0)$或$(-2,0)$。
当A在y轴上时,设A的坐标为$(0,y)$,此时三角形$OAB$的底为$OB$的横坐标的绝对值,即1,高为$|y|$。
同样根据三角形面积公式,我们有$S_{\bigtriangleup OAB} = \frac{1}{2} × 1 × |y| = 2$,
解得$y = \pm 4$,
所以A的坐标可能为$(0,4)$或$(0,-4)$。
综上,满足条件的点A的坐标为$(2,0)$,$(-2,0)$,$(0,4)$,$(0,-4)$。
【答案】:
$(2,0)$,$(-2,0)$,$(0,4)$,$(0,-4)$。
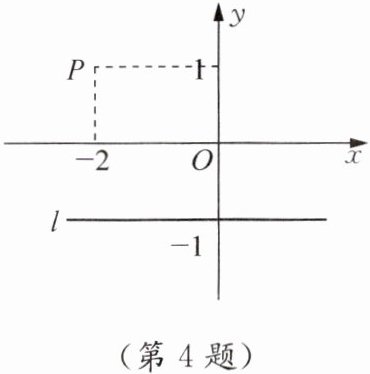
4. 如图,点P(-2,1)与点Q(a,b)关于过点(0,-1)且垂直于y轴的直线l对称,则a+b= ______.

-5
答案:解:过点(0,-1)且垂直于y轴的直线l的方程为y=-1。
点P(-2,1)到直线l的距离为1 - (-1) = 2,所以点Q(a,b)到直线l的距离也为2。
因为点Q在直线l下方,所以b = -1 - 2 = -3。
又因为点P与点Q关于直线l对称,所以两点的横坐标相同,即a = -2。
则a + b = -2 + (-3) = -5。
-5
点P(-2,1)到直线l的距离为1 - (-1) = 2,所以点Q(a,b)到直线l的距离也为2。
因为点Q在直线l下方,所以b = -1 - 2 = -3。
又因为点P与点Q关于直线l对称,所以两点的横坐标相同,即a = -2。
则a + b = -2 + (-3) = -5。
-5
5. 如图,在四边形ABCD中,AD//BC//x轴,下列说法中正确的是(

A.点A与点D的纵坐标相同
B.点A与点B的横坐标相同
C.点A与点C的纵坐标相同
D.点B与点D的横坐标相同
A
).
A.点A与点D的纵坐标相同
B.点A与点B的横坐标相同
C.点A与点C的纵坐标相同
D.点B与点D的横坐标相同
答案:【解析】:本题可根据平行于$x$轴的直线上的点的坐标特征来逐一分析选项。
平行于$x$轴的直线上的所有点的纵坐标都相等。
已知在四边形$ABCD$中,$AD// BC// x$轴,根据上述性质可知:
点$A$与点$D$都在直线$AD$上,而直线$AD$平行于$x$轴,所以点$A$与点$D$的纵坐标相同,A选项正确。
点$A$与点$B$分别在两条不同的平行于$x$轴的直线上,所以它们的横坐标不一定相同,B选项错误。
点$A$与点$C$分别在两条不同的平行于$x$轴的直线上,所以它们的纵坐标不一定相同,C选项错误。
点$B$与点$D$分别在两条不同的平行于$x$轴的直线上,所以它们的横坐标不一定相同,D选项错误。
【答案】:A
平行于$x$轴的直线上的所有点的纵坐标都相等。
已知在四边形$ABCD$中,$AD// BC// x$轴,根据上述性质可知:
点$A$与点$D$都在直线$AD$上,而直线$AD$平行于$x$轴,所以点$A$与点$D$的纵坐标相同,A选项正确。
点$A$与点$B$分别在两条不同的平行于$x$轴的直线上,所以它们的横坐标不一定相同,B选项错误。
点$A$与点$C$分别在两条不同的平行于$x$轴的直线上,所以它们的纵坐标不一定相同,C选项错误。
点$B$与点$D$分别在两条不同的平行于$x$轴的直线上,所以它们的横坐标不一定相同,D选项错误。
【答案】:A
6. 如果点P(5,y)在第四象限,那么y的取值范围是(
A.y≤0
B.y≥0
C.y<0
D.y>0
C
).A.y≤0
B.y≥0
C.y<0
D.y>0
答案:【解析】:
题目考查了平面直角坐标系中各象限的坐标特点。
在平面直角坐标系中,第四象限的点具有特定的坐标特点,即横坐标为正,纵坐标为负。
题目给出了点$P(5,y)$在第四象限,根据第四象限的坐标特点,可以知道纵坐标$y$必须小于0。
【答案】:
C. $y<0$。
题目考查了平面直角坐标系中各象限的坐标特点。
在平面直角坐标系中,第四象限的点具有特定的坐标特点,即横坐标为正,纵坐标为负。
题目给出了点$P(5,y)$在第四象限,根据第四象限的坐标特点,可以知道纵坐标$y$必须小于0。
【答案】:
C. $y<0$。
7. 在平面直角坐标系中,点A绕x轴上一点按顺时针方向旋转90°得到点$A_1,$点A和$A_1$的坐标分别是(0,4)和(5,1),则旋转中心的坐标是(
A.(-1,0)
B.(1,0)
C.(2,0)
D.(1.5,0)
B
).A.(-1,0)
B.(1,0)
C.(2,0)
D.(1.5,0)
答案:【解析】:
本题主要考查了平面直角坐标系中的旋转问题。
设旋转中心的坐标为$(x, 0)$。
点$A(0, 4)$绕旋转中心$(x, 0)$顺时针旋转$90^\circ$得到点$A_1(5, 1)$。
在旋转过程中,点$A$到旋转中心的距离应等于点$A_1$到旋转中心的距离。
计算点$A$到旋转中心的距离的平方:
$OA^2 = (x - 0)^2 + (0 - 4)^2 = x^2 + 16$
计算点$A_1$到旋转中心的距离的平方:
$OA_1^2 = (5 - x)^2 + (1 - 0)^2 = (5 - x)^2 + 1$
由于$OA = OA_1$,我们有:
$x^2 + 16 = (5 - x)^2 + 1$
解这个方程,我们得到:
$x^2 + 16 = 25 - 10x + x^2 + 1$
$16 = 26 - 10x$
$10x = 10$
$x = 1$
因此,旋转中心的坐标是$(1, 0)$。
【答案】:
B. $(1, 0)$
本题主要考查了平面直角坐标系中的旋转问题。
设旋转中心的坐标为$(x, 0)$。
点$A(0, 4)$绕旋转中心$(x, 0)$顺时针旋转$90^\circ$得到点$A_1(5, 1)$。
在旋转过程中,点$A$到旋转中心的距离应等于点$A_1$到旋转中心的距离。
计算点$A$到旋转中心的距离的平方:
$OA^2 = (x - 0)^2 + (0 - 4)^2 = x^2 + 16$
计算点$A_1$到旋转中心的距离的平方:
$OA_1^2 = (5 - x)^2 + (1 - 0)^2 = (5 - x)^2 + 1$
由于$OA = OA_1$,我们有:
$x^2 + 16 = (5 - x)^2 + 1$
解这个方程,我们得到:
$x^2 + 16 = 25 - 10x + x^2 + 1$
$16 = 26 - 10x$
$10x = 10$
$x = 1$
因此,旋转中心的坐标是$(1, 0)$。
【答案】:
B. $(1, 0)$