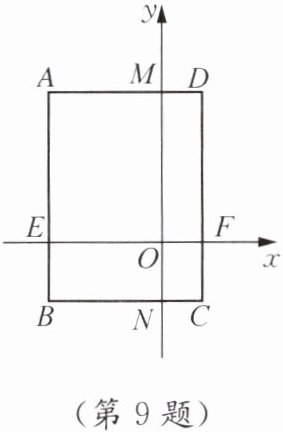
9. 如图,长方形ABCD在平面直角坐标系中的位置如图所示,AD//x轴,AB//y轴,已知AB= 3,BC= 2,且点A的坐标为(-1.5,2),求顶点B,C,D的坐标及四边形AEOM的面积.

答案:解:
∵四边形ABCD是长方形,AD//x轴,AB//y轴,A(-1.5,2),AB=3,BC=2,
∴点B与A横坐标相同,纵坐标为2-3=-1,即B(-1.5,-1);
点D与A纵坐标相同,横坐标为-1.5+2=0.5,即D(0.5,2);
点C与B横坐标相同,与D纵坐标相同,即C(0.5,-1)。
由图知,E为A在x轴上的投影,坐标(-1.5,0);M为D在y轴上的投影,坐标(0,2);O为原点(0,0)。
四边形AEOM为长方形,AE=2-0=2,OE=0-(-1.5)=1.5,
∴面积=AE×OE=2×1.5=3。
顶点坐标:B(-1.5,-1),C(0.5,-1),D(0.5,2);四边形AEOM面积:3。
∵四边形ABCD是长方形,AD//x轴,AB//y轴,A(-1.5,2),AB=3,BC=2,
∴点B与A横坐标相同,纵坐标为2-3=-1,即B(-1.5,-1);
点D与A纵坐标相同,横坐标为-1.5+2=0.5,即D(0.5,2);
点C与B横坐标相同,与D纵坐标相同,即C(0.5,-1)。
由图知,E为A在x轴上的投影,坐标(-1.5,0);M为D在y轴上的投影,坐标(0,2);O为原点(0,0)。
四边形AEOM为长方形,AE=2-0=2,OE=0-(-1.5)=1.5,
∴面积=AE×OE=2×1.5=3。
顶点坐标:B(-1.5,-1),C(0.5,-1),D(0.5,2);四边形AEOM面积:3。
10. 在10×10网格中建立如图所示的平面直角坐标系,△ABC是格点三角形(三角形的顶点是网格线的交点).
(1)画出△ABC关于y轴对称的$△A_1B_1C_1;$
(2)将$△A_1B_1C_1$先向下平移5个单位长度,再向右平移3个单位长度,画出得到的$△A_2B_2C_2;$
(3)若点P(a,b)是△ABC上一点,请写出点P经过上述两次图形变换后的对应点$P_2$的坐标.

(1)画出△ABC关于y轴对称的$△A_1B_1C_1;$
(2)将$△A_1B_1C_1$先向下平移5个单位长度,再向右平移3个单位长度,画出得到的$△A_2B_2C_2;$
(3)若点P(a,b)是△ABC上一点,请写出点P经过上述两次图形变换后的对应点$P_2$的坐标.

答案:【解析】:
本题主要考查了坐标平面中图形的对称变换和平移变换,以及点的坐标变换规律。
(1)关于$y$轴对称的点的坐标特征是横坐标互为相反数,纵坐标不变。因此,只需将$\bigtriangleup ABC$的三个顶点$A$、$B$、$C$分别关于$y$轴对称,得到$A_1$、$B_1$、$C_1$,然后连接这三个点即可得到$\bigtriangleup A_1B_1C_1$。
(2)平移变换的规则是,向下平移$n$个单位,纵坐标减$n$;向右平移$m$个单位,横坐标加$m$。所以,将$\bigtriangleup A_1B_1C_1$的三个顶点$A_1$、$B_1$、$C_1$分别先向下平移$5$个单位长度,再向右平移$3$个单位长度,得到$A_2$、$B_2$、$C_2$,连接这三个点即可得到$\bigtriangleup A_2B_2C_2$。
(3)对于点$P(a,b)$,先关于$y$轴对称,得到点$P_1(-a,b)$,再向下平移$5$个单位长度,纵坐标变为$b-5$,再向右平移$3$个单位长度,横坐标变为$-a+3$,所以$P_2$的坐标为$(-a+3,b-5)$。
【答案】:
(1)图略(按照关于$y$轴对称的规则画出$\bigtriangleup A_1B_1C_1$即可);
(2)图略(按照先向下平移$5$个单位长度,再向右平移$3$个单位长度的规则画出$\bigtriangleup A_2B_2C_2$即可);
(3)$P_2(-a+3,b-5)$。
本题主要考查了坐标平面中图形的对称变换和平移变换,以及点的坐标变换规律。
(1)关于$y$轴对称的点的坐标特征是横坐标互为相反数,纵坐标不变。因此,只需将$\bigtriangleup ABC$的三个顶点$A$、$B$、$C$分别关于$y$轴对称,得到$A_1$、$B_1$、$C_1$,然后连接这三个点即可得到$\bigtriangleup A_1B_1C_1$。
(2)平移变换的规则是,向下平移$n$个单位,纵坐标减$n$;向右平移$m$个单位,横坐标加$m$。所以,将$\bigtriangleup A_1B_1C_1$的三个顶点$A_1$、$B_1$、$C_1$分别先向下平移$5$个单位长度,再向右平移$3$个单位长度,得到$A_2$、$B_2$、$C_2$,连接这三个点即可得到$\bigtriangleup A_2B_2C_2$。
(3)对于点$P(a,b)$,先关于$y$轴对称,得到点$P_1(-a,b)$,再向下平移$5$个单位长度,纵坐标变为$b-5$,再向右平移$3$个单位长度,横坐标变为$-a+3$,所以$P_2$的坐标为$(-a+3,b-5)$。
【答案】:
(1)图略(按照关于$y$轴对称的规则画出$\bigtriangleup A_1B_1C_1$即可);
(2)图略(按照先向下平移$5$个单位长度,再向右平移$3$个单位长度的规则画出$\bigtriangleup A_2B_2C_2$即可);
(3)$P_2(-a+3,b-5)$。