1. 函数$y= -2x+4$的图象不经过(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
C
).A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:【解析】:
本题考察的是一次函数的图象性质。
对于一次函数$y=kx+b$,其中$k$为斜率,$b$为截距。
当$k>0$,$b>0$时,图象经过第一、二、三象限;
当$k<0$,$b>0$时,图象经过第一、二、四象限;
当$k>0$,$b<0$时,图象经过第一、三、四象限;
当$k<0$,$b<0$时,图象经过第二、三、四象限。
对于给定的函数$y=-2x+4$,其中$k=-2<0$,$b=4>0$,所以图象会经过第一、二、四象限,不会经过第三象限。
【答案】:
C
本题考察的是一次函数的图象性质。
对于一次函数$y=kx+b$,其中$k$为斜率,$b$为截距。
当$k>0$,$b>0$时,图象经过第一、二、三象限;
当$k<0$,$b>0$时,图象经过第一、二、四象限;
当$k>0$,$b<0$时,图象经过第一、三、四象限;
当$k<0$,$b<0$时,图象经过第二、三、四象限。
对于给定的函数$y=-2x+4$,其中$k=-2<0$,$b=4>0$,所以图象会经过第一、二、四象限,不会经过第三象限。
【答案】:
C
2. 一次函数的图象如图所示,这个一次函数的表达式是(
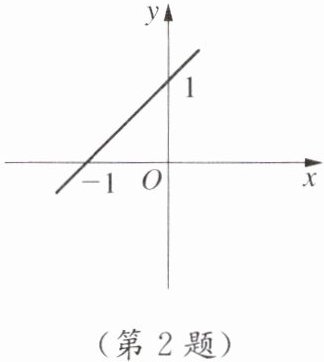
A.$y= -x+1$
B.$y= x-1$
C.$y= -x-1$
D.$y= x+1$
D
).
A.$y= -x+1$
B.$y= x-1$
C.$y= -x-1$
D.$y= x+1$
答案:【解析】:本题考查一次函数图象上点的坐标特征以及待定系数法求一次函数解析式。
从图象上可以看出,该直线经过点$(-1,0)$和$(0,1)$。
设一次函数的表达式为$y = kx + b$(其中$k$和$b$是常数,且$k \neq 0$)。
将点$(-1,0)$代入$y = kx + b$,得到:
$0 = -k + b \quad (方程1)$
将点$(0,1)$代入$y = kx + b$,得到:
$1 = b \quad (方程2)$
由方程2,我们可以直接得出$b = 1$。
将$b = 1$代入方程1,得到:
$0 = -k + 1$
解得:
$k = 1$
因此,一次函数的表达式为$y = x + 1$。
【答案】:D. $y = x + 1$。
从图象上可以看出,该直线经过点$(-1,0)$和$(0,1)$。
设一次函数的表达式为$y = kx + b$(其中$k$和$b$是常数,且$k \neq 0$)。
将点$(-1,0)$代入$y = kx + b$,得到:
$0 = -k + b \quad (方程1)$
将点$(0,1)$代入$y = kx + b$,得到:
$1 = b \quad (方程2)$
由方程2,我们可以直接得出$b = 1$。
将$b = 1$代入方程1,得到:
$0 = -k + 1$
解得:
$k = 1$
因此,一次函数的表达式为$y = x + 1$。
【答案】:D. $y = x + 1$。
3. 一次函数$kx-3y= 8和2x+5y= -4$的图象交点的纵坐标是0,则$k$的值为(
A.4
B.-4
C.2
D.-2
B
).A.4
B.-4
C.2
D.-2
答案:解:因为两函数图象交点的纵坐标是0,所以交点坐标为$(x,0)$。
将$y=0$代入$2x + 5y=-4$,得$2x=-4$,解得$x=-2$。
所以交点坐标为$(-2,0)$。
将$x=-2$,$y=0$代入$kx - 3y=8$,得$-2k=8$,解得$k=-4$。
答案:B
将$y=0$代入$2x + 5y=-4$,得$2x=-4$,解得$x=-2$。
所以交点坐标为$(-2,0)$。
将$x=-2$,$y=0$代入$kx - 3y=8$,得$-2k=8$,解得$k=-4$。
答案:B
4. 如图所示的计算程序中,$y关于x$的函数关系所对应的图象应为(


D
).

答案:解:由计算程序得,y=(-x)×2+4=-2x+4。
当x=0时,y=4;当y=0时,-2x+4=0,x=2。
函数y=-2x+4的图象过点(0,4)和(2,0),对应选项D。
答案:D
当x=0时,y=4;当y=0时,-2x+4=0,x=2。
函数y=-2x+4的图象过点(0,4)和(2,0),对应选项D。
答案:D
5. 某快餐店日均售出各类午饭套餐400份,其中招牌套餐每份为10元,其余套餐每份为8元.若平均每天售出招牌套餐$x$份,卖午饭套餐总收入为$y$元,则$y关于x$的函数表达式是(
A.$y= 18x$
B.$y= 2x+3200$
C.$y= 18x+3200$
D.$y= -18x+3200$
B
).A.$y= 18x$
B.$y= 2x+3200$
C.$y= 18x+3200$
D.$y= -18x+3200$
答案:解:由题意,得其余套餐售出$(400 - x)$份。
招牌套餐收入为$10x$元,其余套餐收入为$8(400 - x)$元。
总收入$y = 10x + 8(400 - x)$
$= 10x + 3200 - 8x$
$= 2x + 3200$
答案:B
招牌套餐收入为$10x$元,其余套餐收入为$8(400 - x)$元。
总收入$y = 10x + 8(400 - x)$
$= 10x + 3200 - 8x$
$= 2x + 3200$
答案:B
6. 点$A(-5,y_{1})和点B(-2,y_{2})都在一次函数y= -\frac{1}{2}x$的图象上,则$y_{1}与y_{2}$的关系是(
A.$y_{1}\leqslant y_{2}$
B.$y_{1}= y_{2}$
C.$y_{1}\lt y_{2}$
D.$y_{1}>y_{2}$
D
).A.$y_{1}\leqslant y_{2}$
B.$y_{1}= y_{2}$
C.$y_{1}\lt y_{2}$
D.$y_{1}>y_{2}$
答案:解:因为点$A(-5,y_{1})$在一次函数$y=-\frac{1}{2}x$的图象上,所以将$x=-5$代入函数得:$y_{1}=-\frac{1}{2}×(-5)=\frac{5}{2}$。
因为点$B(-2,y_{2})$在一次函数$y=-\frac{1}{2}x$的图象上,所以将$x=-2$代入函数得:$y_{2}=-\frac{1}{2}×(-2)=1$。
因为$\frac{5}{2}>1$,所以$y_{1}>y_{2}$。
D
因为点$B(-2,y_{2})$在一次函数$y=-\frac{1}{2}x$的图象上,所以将$x=-2$代入函数得:$y_{2}=-\frac{1}{2}×(-2)=1$。
因为$\frac{5}{2}>1$,所以$y_{1}>y_{2}$。
D
7. 已知点$A(1,m)$在一次函数$y= 3x-2$的图象上,则$m= $
1
.答案:解:因为点$A(1,m)$在一次函数$y = 3x - 2$的图象上,所以将$x = 1$代入函数解析式可得:$m = 3×1 - 2 = 1$。
$1$
$1$
8. 已知方程组$\begin{cases}x+y= 1\\2x-y= 2\end{cases} $的解为$\begin{cases}x= 1\\y= 0\end{cases} $,则一次函数$y= -x+1的图象与y= 2x-2$的图象交点的坐标是
$(1, 0)$
.答案:【解析】:
本题主要考查了一次函数与二元一次方程组的关系。
已知方程组$\begin{cases}x+y= 1\\2x-y= 2\end{cases}$的解为$\begin{cases}x= 1\\y= 0\end{cases}$。
这两个方程可以分别转化为一次函数形式:
$y = -x + 1$
$y = 2x - 2$
因此,方程组的解就是这两个一次函数图象的交点坐标。
所以,一次函数$y = -x + 1$的图象与$y = 2x - 2$的图象交点的坐标是$(1, 0)$。
【答案】:
$(1, 0)$
本题主要考查了一次函数与二元一次方程组的关系。
已知方程组$\begin{cases}x+y= 1\\2x-y= 2\end{cases}$的解为$\begin{cases}x= 1\\y= 0\end{cases}$。
这两个方程可以分别转化为一次函数形式:
$y = -x + 1$
$y = 2x - 2$
因此,方程组的解就是这两个一次函数图象的交点坐标。
所以,一次函数$y = -x + 1$的图象与$y = 2x - 2$的图象交点的坐标是$(1, 0)$。
【答案】:
$(1, 0)$
9. 已知一次函数$y= kx+b的图象经过点(0,1)$,且$y随x$的增大而增大,写出一个符合条件的函数表达式:
$y=x + 1$
.答案:解:因为一次函数$y=kx+b$的图象经过点$(0,1)$,所以将$x=0$,$y=1$代入函数表达式可得$1=k×0 + b$,即$b=1$。
又因为$y$随$x$的增大而增大,所以$k>0$。
取$k=1$,则符合条件的函数表达式为$y=x + 1$。
$y=x + 1$
又因为$y$随$x$的增大而增大,所以$k>0$。
取$k=1$,则符合条件的函数表达式为$y=x + 1$。
$y=x + 1$