1. “$x$ 的 $2$ 倍与 $y$ 的差”用代数式可以表示为(
A.$x(2 - y)$
B.$x + 2 - y$
C.$2x - y$
D.$x - 2y$
C
)A.$x(2 - y)$
B.$x + 2 - y$
C.$2x - y$
D.$x - 2y$
答案:C
2. 下列方程中,是一元一次方程的是(
A.$3x + 2y = 5$
B.$y^2 - 6y + 5 = 0$
C.$\frac{1}{3}x - 3 = \frac{1}{x}$
D.$4x - 3 = 0$
D
)A.$3x + 2y = 5$
B.$y^2 - 6y + 5 = 0$
C.$\frac{1}{3}x - 3 = \frac{1}{x}$
D.$4x - 3 = 0$
答案:D
3. 已知方程 $(m - 2)x^{|m| - 1} + 3 = m - 5$ 是关于 $x$ 的一元一次方程,则 $m$ 的值为(
A.$\pm 2$
B.$2$
C.$-2$
D.$5$
C
)A.$\pm 2$
B.$2$
C.$-2$
D.$5$
答案:C
解析:
因为方程$(m - 2)x^{|m| - 1} + 3 = m - 5$是关于$x$的一元一次方程,所以$|m| - 1 = 1$且$m - 2 \neq 0$。
由$|m| - 1 = 1$,得$|m| = 2$,$m = \pm 2$。
由$m - 2 \neq 0$,得$m \neq 2$。
综上,$m = -2$。
C
由$|m| - 1 = 1$,得$|m| = 2$,$m = \pm 2$。
由$m - 2 \neq 0$,得$m \neq 2$。
综上,$m = -2$。
C
4. 已知 $x = y$,下列变形中不一定正确的是(
A.$x - 2 = y - 2$
B.$-2x = -2y$
C.$ax = ay$
D.$\frac{x}{c^2} = \frac{y}{c^2}$
D
)A.$x - 2 = y - 2$
B.$-2x = -2y$
C.$ax = ay$
D.$\frac{x}{c^2} = \frac{y}{c^2}$
答案:D
5. 一件衣服标价 $132$ 元,若以九折降价出售,仍可获利 $10\%$,则这件衣服的进价是(
A.$106$ 元
B.$105$ 元
C.$118$ 元
D.$108$ 元
D
)A.$106$ 元
B.$105$ 元
C.$118$ 元
D.$108$ 元
答案:D
解析:
设这件衣服的进价是$x$元。
衣服标价132元,以九折出售,售价为$132×0.9 = 118.8$元。
因为仍可获利$10\%$,所以售价是进价的$(1 + 10\%)$,即$(1 + 0.1)x = 1.1x$。
由此可得方程:$1.1x = 118.8$,解得$x = 118.8÷1.1 = 108$。
D
衣服标价132元,以九折出售,售价为$132×0.9 = 118.8$元。
因为仍可获利$10\%$,所以售价是进价的$(1 + 10\%)$,即$(1 + 0.1)x = 1.1x$。
由此可得方程:$1.1x = 118.8$,解得$x = 118.8÷1.1 = 108$。
D
6. 下列方程变形中,正确的是(
A.方程 $3x - 2 = 2x + 1$,移项,得 $3x - 2x = -1 + 2$
B.方程 $3 - x = 2 - 5(x - 1)$,去括号,得 $3 - x = 2 - 5x - 1$
C.方程 $\frac{2}{3}x = \frac{3}{2}$,未知数系数化为 $1$,得 $x = 1$
D.方程 $\frac{x - 1}{0.2} - \frac{x}{0.5} = 1$ 化成 $5x - 5 - 2x = 1$
D
)A.方程 $3x - 2 = 2x + 1$,移项,得 $3x - 2x = -1 + 2$
B.方程 $3 - x = 2 - 5(x - 1)$,去括号,得 $3 - x = 2 - 5x - 1$
C.方程 $\frac{2}{3}x = \frac{3}{2}$,未知数系数化为 $1$,得 $x = 1$
D.方程 $\frac{x - 1}{0.2} - \frac{x}{0.5} = 1$ 化成 $5x - 5 - 2x = 1$
答案:D
解析:
A. 方程$3x - 2 = 2x + 1$,移项,得$3x - 2x = 1 + 2$,原变形错误。
B. 方程$3 - x = 2 - 5(x - 1)$,去括号,得$3 - x = 2 - 5x + 5$,原变形错误。
C. 方程$\frac{2}{3}x = \frac{3}{2}$,未知数系数化为$1$,得$x = \frac{3}{2} ÷ \frac{2}{3} = \frac{9}{4}$,原变形错误。
D. 方程$\frac{x - 1}{0.2} - \frac{x}{0.5} = 1$,分子分母同乘$10$化为$\frac{10(x - 1)}{2} - \frac{10x}{5} = 1$,即$5(x - 1) - 2x = 1$,去括号得$5x - 5 - 2x = 1$,变形正确。
结论:D
B. 方程$3 - x = 2 - 5(x - 1)$,去括号,得$3 - x = 2 - 5x + 5$,原变形错误。
C. 方程$\frac{2}{3}x = \frac{3}{2}$,未知数系数化为$1$,得$x = \frac{3}{2} ÷ \frac{2}{3} = \frac{9}{4}$,原变形错误。
D. 方程$\frac{x - 1}{0.2} - \frac{x}{0.5} = 1$,分子分母同乘$10$化为$\frac{10(x - 1)}{2} - \frac{10x}{5} = 1$,即$5(x - 1) - 2x = 1$,去括号得$5x - 5 - 2x = 1$,变形正确。
结论:D
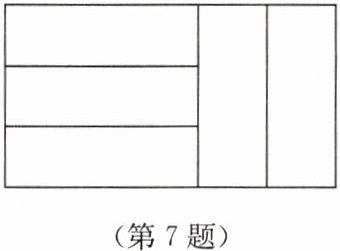
7. 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是 $32$ cm,则小长方形的面积是(
A.$8$ $cm^2$
B.$10$ $cm^2$
C.$12$ $cm^2$
D.$60$ $cm^2$
C
)
A.$8$ $cm^2$
B.$10$ $cm^2$
C.$12$ $cm^2$
D.$60$ $cm^2$
答案:C
解析:
设小长方形的长为$x$ cm,宽为$y$ cm。
由图可知:$3y = x$,大长方形的长为$x + 2y$,宽为$x$。
大长方形周长:$2[(x + 2y) + x] = 32$,即$2(2x + 2y) = 32$,化简得$x + y = 8$。
将$x = 3y$代入$x + y = 8$,得$3y + y = 8$,$4y = 8$,$y = 2$。
则$x = 3y = 6$。
小长方形面积:$x × y = 6 × 2 = 12$ $cm^2$。
C
由图可知:$3y = x$,大长方形的长为$x + 2y$,宽为$x$。
大长方形周长:$2[(x + 2y) + x] = 32$,即$2(2x + 2y) = 32$,化简得$x + y = 8$。
将$x = 3y$代入$x + y = 8$,得$3y + y = 8$,$4y = 8$,$y = 2$。
则$x = 3y = 6$。
小长方形面积:$x × y = 6 × 2 = 12$ $cm^2$。
C
8. 下边给出的是某月的日历表,任意圈出一竖列上相邻的三个数,请你运用方程思想来研究,发现这三个数的和不可能是(

A.$69$
B.$40$
C.$27$
D.$54$
B
)
A.$69$
B.$40$
C.$27$
D.$54$
答案:B
解析:
设中间的数为$x$,则上面的数为$x - 7$,下面的数为$x + 7$。
三个数的和为:$(x - 7) + x + (x + 7) = 3x$,即三个数的和是$3$的倍数。
A. $69÷3 = 23$,是$3$的倍数;
B. $40÷3\approx13.33$,不是$3$的倍数;
C. $27÷3 = 9$,是$3$的倍数;
D. $54÷3 = 18$,是$3$的倍数。
B
三个数的和为:$(x - 7) + x + (x + 7) = 3x$,即三个数的和是$3$的倍数。
A. $69÷3 = 23$,是$3$的倍数;
B. $40÷3\approx13.33$,不是$3$的倍数;
C. $27÷3 = 9$,是$3$的倍数;
D. $54÷3 = 18$,是$3$的倍数。
B
9. 方程 $-\frac{2}{3}x = 4$ 的解为
x=-6
。答案:x=-6
解析:
解:方程两边同时乘以$-\frac{3}{2}$,得$x = 4×(-\frac{3}{2})$,计算得$x=-6$。
10. 当 $n = $
2
时,单项式 $7x^2y^{2n + 1}$ 与 $-\frac{1}{3}x^2y^5$ 是同类项。答案:2
解析:
因为单项式$7x^2y^{2n + 1}$与$-\frac{1}{3}x^2y^5$是同类项,所以相同字母的指数相同,即$2n + 1 = 5$,解得$n = 2$。
2
2
11. 若关于 $x$ 的方程 $2(x + a) = x$ 的解是 $x = 2$,则 $a$ 的值是
-1
。答案:-1
解析:
将$x = 2$代入方程$2(x + a)=x$,得$2(2 + a)=2$。
方程两边同时除以$2$:$2 + a=1$。
移项可得:$a=1 - 2$,即$a=-1$。
-1
方程两边同时除以$2$:$2 + a=1$。
移项可得:$a=1 - 2$,即$a=-1$。
-1
12. 若 $3x - 2$ 和 $4 - 5x$ 互为相反数,则 $x = $
1
。答案:1
解析:
解:因为$3x - 2$和$4 - 5x$互为相反数,所以$3x - 2 + 4 - 5x = 0$,
合并同类项得:$-2x + 2 = 0$,
移项得:$-2x = -2$,
系数化为$1$得:$x = 1$。
1
合并同类项得:$-2x + 2 = 0$,
移项得:$-2x = -2$,
系数化为$1$得:$x = 1$。
1