2. 如图,下列语句:① 直线$ l 经过 C $,$ D $两点;② 点$ C $,$ D 在直线 l $上;③ 直线$ l 是由 C $,$ D $两点确定的;④ $ l $是一条直线,$ C $,$ D $是任意两点. 其中正确的有
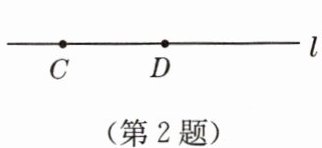
①②③
.(填序号)
答案:①②③.
3. 如图,图中的射线有

AB,BA,BC,CB
,图中的线段有AB,AC,BC
.(请写出能用图中字母表示的)
答案:AB,BA,BC,CB;AB,AC,BC.
4. 下列说法中正确的是(
A.射线$ EF 和射线 FE $是同一条射线
B.延长线段$ EF 和延长线段 FE $的含义是相同的
C.经过两点可以画一条直线,并且只能画一条直线
D.延长直线$ EF $
C
)A.射线$ EF 和射线 FE $是同一条射线
B.延长线段$ EF 和延长线段 FE $的含义是相同的
C.经过两点可以画一条直线,并且只能画一条直线
D.延长直线$ EF $
答案:C.
问题 (1)同一平面上有 3 条直线$ a $,$ b $,$ c $,它们可能会有几个交点?请画出所有情形,并说明交点的个数.
(2)同一平面上有$ n $条直线两两相交,最少会形成______个交点,最多会形成______个交点.
名师指导
直线的位置关系不明确,应分情况讨论,画出图形是解题的关键.
解题示范 (学生在教师指导下,独立完成)
解:
(2)同一平面上有$ n $条直线两两相交,最少会形成______个交点,最多会形成______个交点.
名师指导
直线的位置关系不明确,应分情况讨论,画出图形是解题的关键.
解题示范 (学生在教师指导下,独立完成)
解:
(1)
情况一:三条直线互相平行,交点个数为$0$个;
情况二:三条直线相交于一点,交点个数为$1$个;
情况三:两条直线平行,第三条直线与这两条平行线相交,交点个数为$2$个;
情况四:三条直线两两相交且不共点,交点个数为$3$个。
(2)
最少会形成$0$个交点;
最多会形成$\frac{n(n - 1)}{2}$个交点。
情况一:三条直线互相平行,交点个数为$0$个;
情况二:三条直线相交于一点,交点个数为$1$个;
情况三:两条直线平行,第三条直线与这两条平行线相交,交点个数为$2$个;
情况四:三条直线两两相交且不共点,交点个数为$3$个。
(2)
最少会形成$0$个交点;
最多会形成$\frac{n(n - 1)}{2}$个交点。
答案:(1)
情况一:三条直线互相平行,交点个数为$0$个;
情况二:三条直线相交于一点,交点个数为$1$个;
情况三:两条直线平行,第三条直线与这两条平行线相交,交点个数为$2$个;
情况四:三条直线两两相交且不共点,交点个数为$3$个。
(2)
最少会形成$0$个交点;
最多会形成$\frac{n(n - 1)}{2}$个交点。
情况一:三条直线互相平行,交点个数为$0$个;
情况二:三条直线相交于一点,交点个数为$1$个;
情况三:两条直线平行,第三条直线与这两条平行线相交,交点个数为$2$个;
情况四:三条直线两两相交且不共点,交点个数为$3$个。
(2)
最少会形成$0$个交点;
最多会形成$\frac{n(n - 1)}{2}$个交点。
1. 描述右图中直线$ l 与点 A $,$ B $的位置关系:
(1)
(2)

(1)
点A在直线l上
或直线l经过点A
;(2)
点B在直线l外
或直线l不经过点B
.
答案:(1)点A在直线l上,直线l经过点A;(2)点B在直线l外,直线l不经过点B.