2. 按下列语句画图:
(1)点$ P 不在直线 l $上;
(2)直线$ a $,$ b 相交于点 E $,点$ F 不在直线 a $,$ b $上;
(3)直线$ l 和直线 a $,$ b 分别交于 A $,$ B $两点;
(4)直线$ a 经过点 A $,但不经过点$ B $;
(5)线段$ AB $,$ CD $,$ EF 相交于点 A $;
(6)在直线$ l 的两侧分别取 A $,$ B $两点,使直线$ AB 与直线 l 相交于点 D $,过点$ D 再作任一直线 a $,但不能过点$ A $,且不与直线$ l $重合;
(7)在同一平面内有 4 个点$ A $,$ B $,$ C $,$ D $,过其中 2 个点画直线.
(1)点$ P 不在直线 l $上;
(2)直线$ a $,$ b 相交于点 E $,点$ F 不在直线 a $,$ b $上;
(3)直线$ l 和直线 a $,$ b 分别交于 A $,$ B $两点;
(4)直线$ a 经过点 A $,但不经过点$ B $;
(5)线段$ AB $,$ CD $,$ EF 相交于点 A $;
(6)在直线$ l 的两侧分别取 A $,$ B $两点,使直线$ AB 与直线 l 相交于点 D $,过点$ D 再作任一直线 a $,但不能过点$ A $,且不与直线$ l $重合;
(7)在同一平面内有 4 个点$ A $,$ B $,$ C $,$ D $,过其中 2 个点画直线.
答案:(1) 图示:点$P$与直线$l$,点$P$不在直线$l$上。
(画一条直线标记为$l$,在直线$l$外任取一点标记为$P$)。
(2) 图示:两条相交直线$a$和$b$,交于点$E$,另取一点$F$不在直线$a$和$b$上。
(画两条相交直线,交点标记为$E$,在两直线外任取一点标记为$F$)。
(3) 图示:直线$l$与直线$a$,$b$分别交于点$A$,$B$。
(画三条直线,其中直线$l$与直线$a$交于点$A$,直线$l$与直线$b$交于点$B$)。
(4) 图示:直线$a$经过点$A$,不经过点$B$。
(画一条直线标记为$a$,在直线$a$上取一点$A$,另取一点$B$不在直线$a$上)。
(5) 图示:三条线段$AB$,$CD$,$EF$相交于点$A$。
(画三条线段,都以$A$为端点或交点,分别标记为$AB$,$CD$(其中$C$和$D$为另外两点,$CD$交$AB$于$A$),$EF$(其中$E$和$F$为另外两点,$EF$交$AB$于$A$))。
(6) 图示:直线$l$,两侧分别有点$A$,$B$,直线$AB$与直线$l$交于点$D$,过点$D$作直线$a$,不过点$A$且不与直线$l$重合。
(画一条直线标记为$l$,在直线$l$两侧分别取点$A$和$B$,连接$A$和$B$,交直线$l$于点$D$,过点$D$作另一条直线标记为$a$,确保直线$a$不过点$A$且不与直线$l$重合)。
(7) 图示(分三种情况):
情况一:四点在同一直线上,画一条直线穿过$A$,$B$,$C$,$D$。
情况二:三点在同一直线上,另一点不在,画一条直线穿过$A$,$B$,$C$,另画三条直线分别穿过$D$与$A$,$B$,$C$中的每一个点(如果$D$不与$A$,$B$,$C$共线)。
情况三:任意三点均不在同一直线上,画六条直线分别穿过$A$与$B$,$A$与$C$,$A$与$D$,$B$与$C$,$B$与$D$,$C$与$D$。
(画一条直线标记为$l$,在直线$l$外任取一点标记为$P$)。
(2) 图示:两条相交直线$a$和$b$,交于点$E$,另取一点$F$不在直线$a$和$b$上。
(画两条相交直线,交点标记为$E$,在两直线外任取一点标记为$F$)。
(3) 图示:直线$l$与直线$a$,$b$分别交于点$A$,$B$。
(画三条直线,其中直线$l$与直线$a$交于点$A$,直线$l$与直线$b$交于点$B$)。
(4) 图示:直线$a$经过点$A$,不经过点$B$。
(画一条直线标记为$a$,在直线$a$上取一点$A$,另取一点$B$不在直线$a$上)。
(5) 图示:三条线段$AB$,$CD$,$EF$相交于点$A$。
(画三条线段,都以$A$为端点或交点,分别标记为$AB$,$CD$(其中$C$和$D$为另外两点,$CD$交$AB$于$A$),$EF$(其中$E$和$F$为另外两点,$EF$交$AB$于$A$))。
(6) 图示:直线$l$,两侧分别有点$A$,$B$,直线$AB$与直线$l$交于点$D$,过点$D$作直线$a$,不过点$A$且不与直线$l$重合。
(画一条直线标记为$l$,在直线$l$两侧分别取点$A$和$B$,连接$A$和$B$,交直线$l$于点$D$,过点$D$作另一条直线标记为$a$,确保直线$a$不过点$A$且不与直线$l$重合)。
(7) 图示(分三种情况):
情况一:四点在同一直线上,画一条直线穿过$A$,$B$,$C$,$D$。
情况二:三点在同一直线上,另一点不在,画一条直线穿过$A$,$B$,$C$,另画三条直线分别穿过$D$与$A$,$B$,$C$中的每一个点(如果$D$不与$A$,$B$,$C$共线)。
情况三:任意三点均不在同一直线上,画六条直线分别穿过$A$与$B$,$A$与$C$,$A$与$D$,$B$与$C$,$B$与$D$,$C$与$D$。
3. 下列说法:① 延长直线$ AB $;② 延长线段$ BA $;③ 延长射线$ OA $;④ 反向延长射线$ OA $;⑤ 反向延长线段$ AB $. 其中,正确说法的个数是(
A.4
B.3
C.2
D.1
B
)A.4
B.3
C.2
D.1
答案:B.
解析:
② 延长线段 $ BA $;④ 反向延长射线 $ OA $;⑤ 反向延长线段 $ AB $ 正确。
B
B
4. 如图,图中有
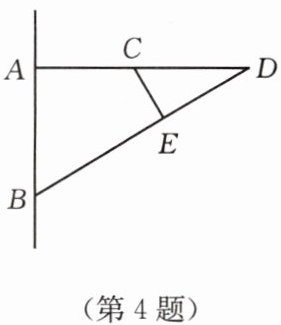
8
条线段,它们是AB,AC,AD,BD,BE,CD,CE,DE
;可用图中字母表示且以$ A $点为端点的射线是射线AB
;图中的直线是直线AB
.
答案:8;AB,AC,AD,BD,BE,CD,CE,DE;射线AB;直线AB.
5. 棋盘上有黑、白两色棋子若干,若把颜色相同的三颗棋子在同一条直线上看作一条直线. 请你根据图示,判断满足这种条件的直线共有

3
条.
答案:3.
6. 如图,乘火车从 A 站出发,沿途经过 3 个车站可到达 B 站,那么在 A、B 两地之间需要安排
20
种不同的车票.
答案:20.
解析:
从A站出发,沿途经过3个车站到达B站,共有5个车站,分别记为A、C、D、E、B。
每个车站到其他车站都有不同的车票,且车票有方向性。
计算单程车票种类:从5个车站中任选2个车站的排列数,即$A_{5}^{2}=5×4=20$。
所以A、B两地之间需要安排20种不同的车票。
20
每个车站到其他车站都有不同的车票,且车票有方向性。
计算单程车票种类:从5个车站中任选2个车站的排列数,即$A_{5}^{2}=5×4=20$。
所以A、B两地之间需要安排20种不同的车票。
20
已知,1 条直线将平面分成 2 个部分,2 条直线最多可将平面分成 4 个部分,3 条直线最多可将平面分成 7 个部分,4 条直线最多可将平面分成 11 个部分,现有 50 条直线最多可将平面分成
1276
个部分.答案:1276.
解析:
设$n$条直线最多将平面分成$a_n$个部分。
已知:
$a_1 = 2$;
$a_2 = a_1 + 2 = 2 + 2 = 4$;
$a_3 = a_2 + 3 = 4 + 3 = 7$;
$a_4 = a_3 + 4 = 7 + 4 = 11$;
规律为$a_n = a_{n-1} + n$,则$a_n = 1 + \frac{n(n + 1)}{2}$。
当$n = 50$时,$a_{50} = 1 + \frac{50×51}{2} = 1 + 1275 = 1276$。
1276
已知:
$a_1 = 2$;
$a_2 = a_1 + 2 = 2 + 2 = 4$;
$a_3 = a_2 + 3 = 4 + 3 = 7$;
$a_4 = a_3 + 4 = 7 + 4 = 11$;
规律为$a_n = a_{n-1} + n$,则$a_n = 1 + \frac{n(n + 1)}{2}$。
当$n = 50$时,$a_{50} = 1 + \frac{50×51}{2} = 1 + 1275 = 1276$。
1276