1. 下列度分秒运算中,正确的是(
A.48°39′+67°31′= 115°10′
B.90°-70°39′= 20°21′
C.21°17′×5= 185°5′
D.180°÷7= 25°43′(精确到分)
D
)A.48°39′+67°31′= 115°10′
B.90°-70°39′= 20°21′
C.21°17′×5= 185°5′
D.180°÷7= 25°43′(精确到分)
答案:D
解析:
A. $48°39'+67°31'=116°10'$
B. $90°-70°39'=19°21'$
C. $21°17'×5=106°25'$
D. $180°÷7\approx25°43'$
D
B. $90°-70°39'=19°21'$
C. $21°17'×5=106°25'$
D. $180°÷7\approx25°43'$
D
2. 若∠A= 20°25′,∠B= 20°15′30″,∠C= 20.25°,则有(
A.∠A>∠B>∠C
B.∠B>∠A>∠C
C.∠A>∠C>∠B
D.∠C>∠A>∠B
A
)A.∠A>∠B>∠C
B.∠B>∠A>∠C
C.∠A>∠C>∠B
D.∠C>∠A>∠B
答案:A
解析:
∠A=20°25′=20°+25×($\frac{1}{60}$)°≈20.4167°,∠B=20°15′30″=20°+15×($\frac{1}{60}$)°+30×($\frac{1}{3600}$)°≈20.2583°,∠C=20.25°,20.4167°>20.2583°>20.25°,所以∠A>∠B>∠C。
A
A
3. 第一节课是上午7:50上课,8:35下课,这一节课期间时针转过的角度为
$22^{\circ}30'$
.(用度分秒的形式表示)答案:$22^{\circ}30'$
解析:
从7:50到8:35,经过的时间为45分钟,即$\frac{45}{60} = \frac{3}{4}$小时。
时针每12小时转$360^{\circ}$,则每小时转$\frac{360^{\circ}}{12} = 30^{\circ}$,每分钟转$\frac{30^{\circ}}{60} = 0.5^{\circ}$。
45分钟时针转过的角度为$45 × 0.5^{\circ} = 22.5^{\circ}$,$0.5^{\circ} = 30'$,所以$22.5^{\circ} = 22^{\circ}30'$。
$22^{\circ}30'$
时针每12小时转$360^{\circ}$,则每小时转$\frac{360^{\circ}}{12} = 30^{\circ}$,每分钟转$\frac{30^{\circ}}{60} = 0.5^{\circ}$。
45分钟时针转过的角度为$45 × 0.5^{\circ} = 22.5^{\circ}$,$0.5^{\circ} = 30'$,所以$22.5^{\circ} = 22^{\circ}30'$。
$22^{\circ}30'$
4. 计算:
(1) 48°33′28″+19°56′42″;
(2) 90°-15°43′29″;
(3) 32°15′29″×4;
(4) 79°40′18″÷3.
(1) 48°33′28″+19°56′42″;
(2) 90°-15°43′29″;
(3) 32°15′29″×4;
(4) 79°40′18″÷3.
答案:(1)$68^{\circ}30'10''$;(2)$74^{\circ}16'31''$;(3)$129^{\circ}1'56''$;(4)$26^{\circ}33'26''$.
解析:
(1) $48^{\circ}33'28'' + 19^{\circ}56'42''$
$=(48^{\circ}+19^{\circ}) + (33'+56') + (28''+42'')$
$=67^{\circ} + 89' + 70''$
$=67^{\circ} + 1^{\circ}29' + 1'10''$
$=68^{\circ}30'10''$
(2) $90^{\circ} - 15^{\circ}43'29''$
$=89^{\circ}59'60'' - 15^{\circ}43'29''$
$=(89^{\circ}-15^{\circ}) + (59'-43') + (60''-29'')$
$=74^{\circ}16'31''$
(3) $32^{\circ}15'29''×4$
$=32^{\circ}×4 + 15'×4 + 29''×4$
$=128^{\circ} + 60' + 116''$
$=128^{\circ} + 1^{\circ} + 1'56''$
$=129^{\circ}1'56''$
(4) $79^{\circ}40'18''÷3$
$79^{\circ}÷3 = 26^{\circ}...1^{\circ}$
$1^{\circ}=60'$,$60' + 40' = 100'$
$100'÷3 = 33'...1'$
$1'=60''$,$60'' + 18'' = 78''$
$78''÷3 = 26''$
$=26^{\circ}33'26''$
5时时,钟面上时针和分针的夹角是多少度?从5时起,经过多长时间,时针和分针第一次重合?
答案:$150^{\circ}$;$\frac{300}{11}$分钟.
解析:
钟面上每一大格为$30^{\circ}$,5时时,时针指向5,分针指向12,中间有5个大格,夹角为$5×30^{\circ}=150^{\circ}$。
分针每分钟转$6^{\circ}$,时针每分钟转$0.5^{\circ}$,5时整,时针与分针夹角$150^{\circ}$,设经过$x$分钟第一次重合,可列方程:$6x - 0.5x = 150$,解得$x=\frac{300}{11}$。
$150^{\circ}$;$\frac{300}{11}$分钟.
分针每分钟转$6^{\circ}$,时针每分钟转$0.5^{\circ}$,5时整,时针与分针夹角$150^{\circ}$,设经过$x$分钟第一次重合,可列方程:$6x - 0.5x = 150$,解得$x=\frac{300}{11}$。
$150^{\circ}$;$\frac{300}{11}$分钟.
1. 如图所示的正方形网格中,$\angle ABC$
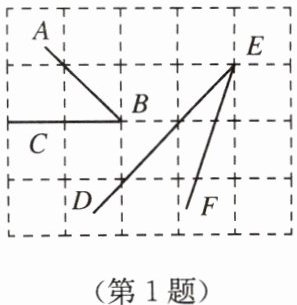
>
$\angle DEF$.(填“$>$”“$=$”或“$<$”)
答案:>
2. 如图,$\because射线OC是\angle AOB$的平分线,$\therefore$

∠AOC
$=$∠BOC
$=\frac{1}{2}$∠AOB
,$\angle AOB= 2$∠AOC
$=2$∠BOC
.
答案:∠AOC,∠BOC,∠AOB;∠AOC,∠BOC