3. (1)如图,$\because \angle AOB= \angle BOC= \angle COD$,$\therefore OB$,$OC$是
(2)如图,$\because \angle AOC= 2\angle AOB$,$\therefore$
(3)如图,$\because \angle BOC= \angle COD= \frac{1}{2}$
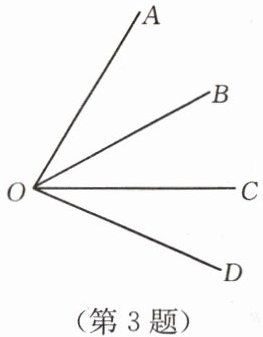
∠AOD
的三
等分线;(2)如图,$\because \angle AOC= 2\angle AOB$,$\therefore$
OB
是∠AOC
的角平分线;(3)如图,$\because \angle BOC= \angle COD= \frac{1}{2}$
∠BOD
,$\therefore$OC
是∠BOD
的角平分线.
答案:(1)∠AOD,三;(2)OB,∠AOC;(3)∠BOD,OC,∠BOD
解析:
(1)$\angle AOD$,三;
(2)$OB$,$\angle AOC$;
(3)$\angle BOD$,$OC$,$\angle BOD$
(2)$OB$,$\angle AOC$;
(3)$\angle BOD$,$OC$,$\angle BOD$
4. 如图,$OC$,$OD分别是\angle AOB$,$\angle BOE$的平分线.
(1)如果$\angle AOB= 70^{\circ}$,$\angle BOE= 60^{\circ}$,那么$\angle 1+\angle 2= $
(2)如果$\angle 1+\angle 2= 55^{\circ}$,则$\angle AOE= $

(1)如果$\angle AOB= 70^{\circ}$,$\angle BOE= 60^{\circ}$,那么$\angle 1+\angle 2= $
65°
;(2)如果$\angle 1+\angle 2= 55^{\circ}$,则$\angle AOE= $
110°
.
答案:(1)65°;(2)110°
解析:
(1)因为OC是$\angle AOB$的平分线,$\angle AOB = 70°$,所以$\angle 1=\frac{1}{2}\angle AOB=\frac{1}{2}×70° = 35°$。
因为OD是$\angle BOE$的平分线,$\angle BOE = 60°$,所以$\angle 2=\frac{1}{2}\angle BOE=\frac{1}{2}×60°=30°$。
则$\angle 1+\angle 2=35° + 30°=65°$。
(2)因为OC是$\angle AOB$的平分线,所以$\angle AOB = 2\angle 1$。
因为OD是$\angle BOE$的平分线,所以$\angle BOE=2\angle 2$。
$\angle AOE=\angle AOB+\angle BOE=2\angle 1 + 2\angle 2=2(\angle 1+\angle 2)$。
已知$\angle 1+\angle 2 = 55°$,所以$\angle AOE=2×55° = 110°$。
(1)$65°$;(2)$110°$
因为OD是$\angle BOE$的平分线,$\angle BOE = 60°$,所以$\angle 2=\frac{1}{2}\angle BOE=\frac{1}{2}×60°=30°$。
则$\angle 1+\angle 2=35° + 30°=65°$。
(2)因为OC是$\angle AOB$的平分线,所以$\angle AOB = 2\angle 1$。
因为OD是$\angle BOE$的平分线,所以$\angle BOE=2\angle 2$。
$\angle AOE=\angle AOB+\angle BOE=2\angle 1 + 2\angle 2=2(\angle 1+\angle 2)$。
已知$\angle 1+\angle 2 = 55°$,所以$\angle AOE=2×55° = 110°$。
(1)$65°$;(2)$110°$
5. 如图,将一副三角板放在一起,使直角顶点重合于点$O$.求$\angle AOC+\angle DOB$的度数.


答案:解:∠AOC+∠DOB=∠AOD+∠COD+∠DOB=∠AOB+∠DOC=180°.
解析:
解:$\angle AOC + \angle DOB = \angle AOD + \angle COD + \angle DOB = \angle AOB + \angle DOC$。
因为一副三角板的直角顶点重合于点$O$,所以$\angle AOB = 90°$,$\angle DOC = 90°$。
因此,$\angle AOC + \angle DOB = 90° + 90° = 180°$。
因为一副三角板的直角顶点重合于点$O$,所以$\angle AOB = 90°$,$\angle DOC = 90°$。
因此,$\angle AOC + \angle DOB = 90° + 90° = 180°$。
问题 如图,$\angle AOC= \angle BOD= 100^{\circ}$.
(1)$\angle AOB与\angle COD$相等吗?为什么?
(2)$\angle AOD与\angle BOC$的和是多少度?

名师指导
(1)根据等式的性质,在等式$\angle AOC= \angle BOD的两边同时减去\angle BOC$.
(2)将$\angle AOD+\angle BOC转化为\angle AOC+\angle COD+\angle BOC$,再转化为$\angle AOC+\angle BOD$求解.
解题示范(学生在教师指导下,独立完成)
解:
(1)$\angle AOB与\angle COD$相等吗?为什么?
(2)$\angle AOD与\angle BOC$的和是多少度?

名师指导
(1)根据等式的性质,在等式$\angle AOC= \angle BOD的两边同时减去\angle BOC$.
(2)将$\angle AOD+\angle BOC转化为\angle AOC+\angle COD+\angle BOC$,再转化为$\angle AOC+\angle BOD$求解.
解题示范(学生在教师指导下,独立完成)
解:
答案:(1)相等。
因为∠AOC=∠BOD=100°,
所以∠AOC - ∠BOC = ∠BOD - ∠BOC,
即∠AOB=∠COD。
(2)∠AOD + ∠BOC
= (∠AOC + ∠COD) + ∠BOC
= ∠AOC + (∠COD + ∠BOC)
= ∠AOC + ∠BOD
= 100° + 100° = 200°。
因为∠AOC=∠BOD=100°,
所以∠AOC - ∠BOC = ∠BOD - ∠BOC,
即∠AOB=∠COD。
(2)∠AOD + ∠BOC
= (∠AOC + ∠COD) + ∠BOC
= ∠AOC + (∠COD + ∠BOC)
= ∠AOC + ∠BOD
= 100° + 100° = 200°。
1. 在$\angle AOB的内部任取一点C$,作射线$OC$,那么有(
A.$\angle AOC= \angle BOC$
B.$\angle AOC>\angle BOC$
C.$\angle BOC>\angle AOB$
D.$\angle AOB>\angle AOC$
D
)A.$\angle AOC= \angle BOC$
B.$\angle AOC>\angle BOC$
C.$\angle BOC>\angle AOB$
D.$\angle AOB>\angle AOC$
答案:D
解析:
在∠AOB内部任取一点C作射线OC,射线OC将∠AOB分成∠AOC和∠BOC两部分,所以∠AOB=∠AOC+∠BOC,因此∠AOB>∠AOC。
D
D