2. 如图,在同一平面内,$\angle AOB= 40^{\circ}$,从顶点$O画一条射线OP$,若$\angle POB= 10^{\circ}$,则$\angle AOP$的度数为()

A.$10^{\circ}$
B.$30^{\circ}$
C.$20^{\circ}或50^{\circ}$
D.$30^{\circ}或50^{\circ}$

3. 阅读下面的题目及解答过程,并填空：
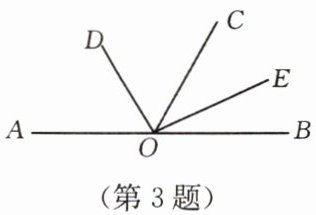
如图,$O是直线AB$上的一点,过$O点作射线OC$,$OD$,$OE$,$OD$平分$\angle AOC$,$OE$平分$\angle BOC$.
(1)如果$\angle AOC= 120^{\circ}$,求$\angle DOE$的度数.
解：$\because OD是\angle AOC$的平分线,$\angle AOC= 120^{\circ}$,
$\therefore \angle DOC= \frac{1}{2}$$=$$^{\circ}$().
$\because OE是\angle BOC$的平分线,$\angle BOC= 180^{\circ}-\angle AOC= 180^{\circ}-120^{\circ}=60^{\circ}$,
同理,$\angle COE= \frac{1}{2}$$=$$^{\circ}$().
$\therefore \angle DOE= $$+$$=$$^{\circ}$.
(2)如果$\angle AOC= n^{\circ}$,则$\angle DOE= $$^{\circ}$.

4. 如图,$OD是\angle AOC$的平分线,$\angle AOD= 40^{\circ}$,$\angle BOD= 70^{\circ}$,求$\angle BOC$的度数.

5. 已知$\angle AOB= 70^{\circ}$,$\angle BOC= 40^{\circ}$,$OD是\angle AOC$的平分线,求$\angle BOD$的度数.

给出如下定义：如果$\angle AOC+\angle BOC= 90^{\circ}$,且$\angle AOC= k\angle BOC$($k$为正整数),那么称$\angle AOC是\angle BOC$的“倍锐角”.
(1)下列三个条件中,能判断$\angle AOC是\angle BOC$的“倍锐角”的是______(填写序号)；
①$\angle BOC= 15^{\circ}$；②$\angle AOC= 70^{\circ}$；③$OC是\angle AOB$的角平分线；
(2)如图①,当$\angle BOC= 30^{\circ}$时,在图中画出$\angle BOC$的一个“倍锐角”$\angle AOC$.
(3)如图②,当$\angle BOC= 60^{\circ}$时,若将射线$OB绕点O$旋转,每次旋转$10^{\circ}$,在旋转过程中可得它的“倍锐角”$\angle AOC= $______.
(4)当$\angle BOC= m^{\circ}$且存在它的“倍锐角”$\angle AOC$时,则$\angle AOB= $______.